Enabling Cross-Chain Transactions: A Decentralized Cryptocurrency Exchange Protocol

Posted on 2021-10-10 Edited on 2021-10-26

赋能跨链交易：一项分布式的加密货币交易协议

**摘要：**受比特币的启发，市场上出现了多种基于区块链技术的加密货币。由于区块链的特殊结构，传统货币与加密货币之间或不同类型加密货币之间的直接交易被认为是不可能的。
通常，不同货币之间的交易是通过一个中心化的第三方平台进行的。但是，它存在单点故障的问题，容易受到攻击，从而影响交易的安全性。在本文中，我们提出了一种分布式加密货币交易方案来解决中心化交易所的问题，可以实现不同类型加密货币之间的安全交易。我们的方案是通过以太坊区块链上的智能合约实现的，并部署在以太坊测试网络上。除了实现单个用户之间的交易，我们的方案还允许多个用户之间的交易。实验结果证明我们方案的成本是可以接受的。

I. 简介

比特币 [1] 是目前最受欢迎的加密货币，自 2009 年部署以来一直运行良好。与传统货币不同，比特币不依赖中央发行人进行管理，而是运行在 P2P（点对点）网络之上，这意味着没有中央机构可以完全控制比特币。
它的交易数据并不存储在中央数据库中，而是写入一个名为区块链blockchian的分布式哈希链中。近年来，受比特币的启发，出现了各种基于区块链的加密货币，例如莱特币 [2] 和以太坊 [3]。为了帮助用户管理不同种类的加密货币，最近的一些工作中通常使用基于可信第三方的中心化交换，例如[4]-[8]。

一方面，通过利用不同的区块链技术，不同种类的加密货币被部署在不同的区块链中。相同货币之间的交易可以通过区块链客户端直接在网络上进行。但是，部署在不同区块链上的加密货币不能直接相互交易。此外，如果用户想使用传统货币购买某种加密货币或将其加密货币转换为现金，则用户只能与第三方进行兑换。在这种情况下，基于可信第三方的交易所是有帮助的，它可以充当中介，帮助用户在不同类型的加密货币之间进行交易。

另一方面，加密货币的所有者通常通过绑定到始终存储在他/她的私人设备中的一对密钥的地址来管理他/她的资产。在这种情况下，一旦设备出现故障、丢失甚至被针对加密货币的恶意软件攻击，用户就会遭受财产损失。
因此需要一个中央组织来帮助用户管理他们的财产。中心化交易所扮演着这个角色，它不仅可以作为加密货币交易的平台，还可以为用户提供一个存放财产的地方。就像银行一样，中心化交易所为用户提供了管理资金和进行交易的便利。现在世界上有 4,000 多个中心化交易所，例如韩国的 Bithumb [9]，每天交易超过 10 亿美元的加密货币。

中心化交易所虽然为用户交易提供了便利，但也带来了一些安全隐患。一旦用户将自己的财产存放在一个中心化的交易平台中，就意味着该交易平台是系统的“阿喀琉斯之踵”，可能会导致用户的财产和交易信息被恶意利用。此外，作为中央机构[10]、[11]，总会存在单点故障。解决这个问题最好的办法是采用分布式加密货币交换方案，这也符合加密货币去中心化的思想。

智能合约（Smart Contract） [12]、[13] 是可以在区块链上部署和执行的代码。通过智能合约，我们能够实现各种去中心化的应用程序。目前，以太坊是支持部署智能合约的最大和最受欢迎的区块链平台。用户可以通过交易将他们的智能合约代码发送到以太坊网络，然后由矿工验证并添加到区块链中。保存在区块链中的任何智能合约代码都可以被满足一定条件的用户调用（通过transaction call合约内的方法）。在本文中，我们考虑使用基于以太坊的智能合约来实现一种去中心化的跨加密货币交换方案，该方案可以验证不同用户发送的不同类型的加密货币交易。我们不仅解决单个用户之间的交易，还考虑了多个用户之间进行交易的情况。

在本文中，我们做出了以下主要贡献：

我们提出了一种基于智能合约的去中心化跨加密货币交换方案，通过随机选择的用户作为中介，可以在单用户和多用户场景下实现任意两种加密货币之间的交易。在多用户场景中，多个用户可以在短时间内发起多次转账，建立的合约可以自动收集这些转账并同时完成这些交易。
在我们的方案中，通过工作量证明（PoW, Proof of Work）和存款证明（Proof of Deposit），随机选择不受信任的自愿用户来组织验证委员会。此外，通过使用智能合约收集验证委员会成员的判断结果，我们的方案可以通过以太坊网络验证任何两种不同类型的加密货币之间的交易。进一步分析表明，我们方案的功能性和事务原子性可以通过选择验证委员会的协议设计来保证。
我们在以太坊测试网络上实施和部署我们提出的方案，并在我们的本地机器上评估合约各部分的运行成本。我们的方案优化了多个用户之间同类型加密货币的执行性能。实验结果表明，我们方案的本地运营成本仅受参与者数量的影响，与每个用户的交易数量无关。我们的跨币种交易方案确保部署成本和执行成本在用户可接受的范围内。

我们论文的其余部分组织如下。
第二节介绍了与我们的方案相关的一系列工作。
第三节中介绍了技术预备知识。
第四节介绍我们的系统和安全模型之后，
第五节详细介绍了我们的交叉加密货币交易方案。
第六节提供了我们方案的安全性分析。
第七节展示了我们方案的详细部署和相关的性能分析。
第八节最后总结了我们的工作。

III 初步准备

A. 区块链中的共识算法

在区块链系统中，用来保证分布式节点一致性的技术称为共识算法。目前常用的共识算法主要分为两类。第一个是基于证明的共识，如 PoW [1]、PoS [37]、DPoS [38]、GHOST [39] 等，它要求用户向网络提交一个难题的解决方案。只有经过网络验证的节点才能发布区块，这也是加密货币中常用的共识。
另一种是解决拜占庭问题的传统分布式网络算法，包括PBFT[40]、[41]、RAFT[42]等。在授权/许可区块链（联盟链）的设计中经常使用传统的分布式网络算法

B. 智能合约中的 Gas

使用gas的概念限制了以太坊上部署的智能合约的长度，这也防止了恶意用户故意部署包含无限循环的合约，避免以太坊网络崩溃。Gas 用于衡量智能合约代码中每个步骤的成本。每笔交易都需要包含一个gas限制，即交易消耗的最大gas量，以及用户为每单位gas支付的以太币数量。矿工有权选择先打包哪个交易。支付的交易费用越多，矿工就越有可能打包您的交易，交易得到确认的速度也就越快。 Gas limit 是用户最多需要支付的交易费用，它限制了智能合约不受限制地执行的能力。
在本文中，我们将我们的合约部署到基于以太坊的测试网络，测量每笔交易所需的 gas，并根据当前汇率计算真实的部署和运营成本。

IV. 系统模型、安全模型和设计目标

文中符号定义

符号	描述
$A$	交易付款人
$B$	交易付款人
$C_1$	交易的第一个中介
$C_2$	交易的第二个中介
$coin_1$	付款人所拥有的币
$coin_2$	接收者所要求的币

A. 系统模型

我们的系统模型中有四个主要组件，详细描述如下：

付款人。付款人是想要将加密货币转移给另一个用户的用户。
付款人。收款人是需要转入的用户，但付款人方面没有他/她需要的加密货币类型。
中介。中介是拥有以太坊账户和另一种加密货币账户的用户，并在这些账户中拥有足够的财产用于进行交易。中介机构通过智能合约连接付款人和收款人。中介机构需要加入验证委员会才能参与交易验证过程，这将在第 V-D 节中介绍。
区块链。我们方案的每次执行都涉及三个区块链，其中两个区块链支持付款人和收款人分别使用的加密货币。第三个区块链是以太坊区块链，我们的智能合约是在它上面设计和部署的。

假设我们在以太坊上部署了智能合约，我们进一步假设所有参与我们计划的用户都需要拥有自己的以太坊账户，并且只需要少量的以太币来支付调用合约的费用。同时，在我们的方案中，付款人/收款人不需要有足够的以太币来直接支持他们的交易。对于只需要参与我们方案中的交易的用户，他/她可以作为 SPV（简化支付验证）节点加入区块链网络 [1]。我们认为，要找到一个可以同时支持两种加密货币交易所需的两种加密货币的中介并不容易。
即使存在这样的中介，我们也可以将其视为我们方案中提到的两个中介。
因此，我们使用两个合适的中介，例如 C1 和 C2，分别实现 A 和 B 之间的加密货币交易。此外，每个中介都可以通过钱包、区块链浏览器等工具验证不同种类的加密货币交易。由于需要中介来验证交易，它可以是全节点或 SPV 节点。

在我们的方案中，我们采用弱同步/部分同步的时间假设，这意味着保证消息在一定的时间限制后被传递。在完全异步的网络中，很难区分正常节点和超时传输的恶意节点。
因此，在我们的方案中，将在智能合约中设置一个计时器，以防止恶意节点拒绝提供验证结果，从而区分正常节点和传输超时的恶意节点。

B. 安全模型

我们系统中的恶意用户可能会设置大量账户作为付款人、收款人或中介，发送大量垃圾交易来破坏我们的计划。所有恶意用户都可能通过欺诈合同来串通以获得额外的利益。它们可能的恶意行为如下所示。

恶意付款人或中间人可能会向合约发送欺骗性消息，而不会进行转账或双重支付。
恶意收款人或中间人可以在收到转账后通过诈骗合同来赚取额外的补偿费用。
参与验证委员会的恶意节点（在第 V-D 节中描述）可能会发布错误信息以破坏共识过程。

与恶意节点不同，受信任节点将遵守我们协议的条款来强制执行其行为，以实现跨加密货币交易或通过我们的方案赚取交易费用。由于验证委员会是通过工作量证明选举产生的，我们假设对于想要加入验证委员会的节点，恶意节点的组合算力在任何时候都应该小于总算力的 1/4 .

否则会引入自私挖矿攻击。这种攻击将使恶意节点更有可能产生更多超过自身算力的区块，从而使他们获得比其在验证委员会中拥有的算力百分比更多的席位。

C. 设计目标

我们的目标是在不同类型的加密货币之间设计一个分散的安全传输方案。具体来说，我们的设计目标包括：

去中心化和非pepudiation：我们的方案中不会有任何中心化的第三方。任何参与协议的一方都不能否认自己的行为。任何用户对智能合约的操作都会永久记录在区块链上。
可移植性：在我们的跨链加密货币交易方案中，我们需要支持多种类型的加密货币之间的交易。换句话说，我们的交易方案不受加密货币类型的限制
公平性：即使我们方案的任何一步失败，我们的方案仍然保证系统正常运行，不会损害任何诚实用户的利益。
稳定性：我们的协议需要能够在安全假设下抵御区块链网络中的常见攻击。
可扩展性：在实际交易场景中，不仅有两个单用户之间的交易，也有多个用户之间的交易。在我们的方案中，我们需要支持多用户之间的交易，性能需要可以接受。
原子性：在我们的跨区块链交易方案中，如果各方都遵守协议，那么所有的交换都会发生。然后，没有遵守协议的一方最终会变得更糟，也没有联盟有偏离协议的动机[31]。
安全和活跃：对于共识协议，安全意味着诚实（非拜占庭）节点同意相同的值，活跃意味着交易最终会中止或提交。

V 跨币种交易方案

在本节中，我们首先解释我们的方案如何应用于使用不同加密货币进行交易的两个用户。
然后，我们设计了一种安全的验证方法来验证交易是否完成。
最后，我们将该方案扩展到多个用户通过不同的加密货币进行交易的场景。

A. 概述

在本节中，我们将概述我们的方案，以展示我们如何实现跨不同类型加密货币的交易。我们的方案包括三个阶段：

合同部署阶段。
这个阶段包括我们方案中涉及的三类合约的部署过程。
交易阶段。
该阶段交易的付款人和收款人在中间人的参与下完成跨加密货币交易。在我们的方案中，这个阶段分为单用户交易和多用户交易两种情况。
交易验证阶段。
为了验证以太坊智能合约中其他类型加密货币的交易结果，我们在此阶段通过选择验证委员会来验证交易。

为了说明方便，我们以比特币和莱特币为例。事实上，我们的方案支持任何类型的加密货币之间的交易。
如图 1 所示，为了通过智能合约实现跨加密货币交易，我们需要两个中间人 C1 和 C2，他们可以是网络中的任何人。

图1：方案概述

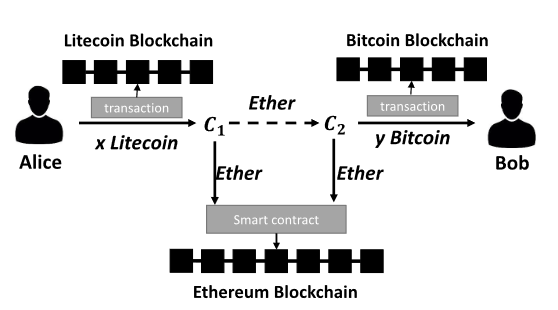
在合约部署阶段，大量合约部署在网络中。然后交易发生在交易阶段。中介机构需要分别支持通过比特币和莱特币进行交易。
首先，A 将 x 莱特币转移到 C1。 C1收到转账后，将等价的ethers转账给C2，然后C2将y个比特币转账给B。这样，我们就以ether的转账作为桥梁，实现了两个用户之间不同加密货币的转账。用户作为中介参与我们合约的动机是他/她可以通过这个过程获得交易费用。

需要注意的是，以太坊除了以太币的转账，还有比特币和莱特币的转账。虽然无法通过以太坊智能合约直接验证这两种货币的交易，但我们通过选择一组用户作为验证委员会来提供验证结果来找到解决方案。在交易验证阶段，合约将整合委员会的判断结果并得出最终结论。正如工作[43]中总结的那样，没有可信的第三方就不可能进行跨链通信，而由分布式节点组成的验证委员会在我们的方案中扮演着这样的角色。

除了上面提到的单用户交易场景，我们还考虑了多用户交易场景。在这种情况下，有多个付款人想要将加密货币转移给一个或多个收款人。我们的合同可以将需要转移相同类型加密货币的付款人与需要不同类型加密货币的收款人结合起来。我们完整提案的细节将在第 V-C.1 至 V-C.2 节中描述。

B. 合约部署阶段

在我们的方案中，使用以太坊的 Solidity 语言编写了三种类型的智能合约。

中介合同。该智能合约主要控制中介的行为，并提供获取中介节点信息的接口。
交易合同。通过该合约，交易的付款人和收款人在中间人的参与下完成了跨加密货币交易。并且这个合约提供了一个调用接口，用于输入验证结果。
委员会合同。该合约用于验证委员会选举，包括 PoW 拼图验证和控制验证委员会的规模，并提供一个接口来验证节点是否是验证委员会的成员。

我们合约的主要功能如下。我们将中介合约表示为 IC，将交易合约表示为 TC，将委员会合约表示为 CC。

表II：智能合约功能

智能合约步骤	功能
IC.Register	中介提供注册信息
IC.Update	中介更新信息
CC.Verify_PoW	验证用户是否有资格加入验证组
TC.Prepare	为交易用户的信息准备
TC.Deposit	用户提交存款
TC.Validation	用户的交易验证

在合约部署阶段，这三类合约在全网大量部署。
用户和中介可以自由选择不超过gas limit的合约进行交易。一旦网络中的交易需求超过合约数量，任何中介也可以进一步部署额外的交易合约和委员会合约。用户可以在中介合约中查询的中介交易信息包括中介机构部署的合约的交易合约地址。一个中介可以部署多个合约。任何中介都可以加入其他合约作为交易所需的两个中介之一。通过不同合约的交易并行发生，因此网络中的交易合约越多，在固定用户数下交易效率就越高

C. 交易阶段

1）单用户交易阶段

在交易阶段，我们首先介绍单用户交易方案。单用户交易方案表示参与交易的双方都是个人。该方案还包括用户与他/她自己的货币兑换（例如，Alice 将她的比特币转换为以太币）。为了清楚起见，我们假设 coin1 和 ether 之间的汇率以及 coin2 和 ether 之间的汇率都是“1”。在实际场景中，非“1”汇率的问题只需要将汇率乘以相应的放大倍数即可。单用户交易方案的主要流程如算法1所示。

// 算法1
输入: 双方及中介的账户地址; 交易金额 x; 汇率; 时间阈值 T;

if 中间人 C1 和 C2 都存入了 Ether
then
    付款人 A 将 x 个 coin1 转给中间人 C1;
    
    if 转账确认成功 then
    	中介C2将xcoin2转给收款人B;
    	
    	if 转账确认成功 then
    		Return 中介C2给自己的押金;
    	else if 超时或确认失败 then
    		将中介C2的押金转给B;
		end
	
		将中介C1的押金转移到C2;

	else if 超时或确认失败 then
		退还中介C1和C2的押金;
	end
	
else if C1 或 C2 没有在时间 T 内提供存款
then
	Return 存入 C1 或 C2 然后终止;
end

在交易开始之前，中介机构将自己支持的加密货币类型和相应的汇率发布到合约中。包括A和B在内的交易双方分别选择合适的中介C1和C2，并将他们的交易信息发布到合约中，例如加密货币类型、交易金额、账户地址等。然后，中介 C1 和 C2 接收双方交易的信息，并通知合约他们选择的用户。然后，他们需要在时间 T 内向合约发送一定数量的押金。如果任何中介未能在 T 时间内提供押金，合约将退还其他中介的押金并停止协议。中介C2收到付款人A向C1转账成功的消息后，向收款人B转账x币2。否则，如果判断A的转账超时或验证失败，则合约退还C1和C2的押金并终止交易交易。如果最终转账交易成功，C2的押金将退还给自己。否则，如果C2的转账被判断为超时或验证失败，则将中介C2保存在合约中的押金发送给B。最终，中介C2将从C1收到x个ether的存款

2）多用户交易阶段

在很多情况下，短时间内可能会有多个用户同时进行交易。我们的智能合约旨在支持多个用户参与加密货币转移。在多用户交易阶段，多个用户可以单独选择自己的交易伙伴。合约将结合这些交易信息，汇总转移给同一用户的加密货币数量，以提高交易效率。多用户交易方案的框架如算法2所示。该方案主要用于一组用户相互交易的场景。智能合约首先收集所有付款人 A1、A2、A3 …An 的信息，并计算出交易金额的总和。中间人 C1 和 C2 收到此信息后，需要选择合适的用户并提交等值的以太币作为押金。如果任何中介未能在 T 时间内提供押金，合约将退还其他中介的押金并停止协议。然后，所有付款人都需要向 C1 支付足够的 coin1。验证委员会的成员需要通过第 V-D 节中描述的方法验证这些转移。转让信息也将记录在合同中。中介 C1 成功收到付款人的转账后，合约计算成功交易的金额，修改 C1 收到的金额，然后将消息发送给 C2。否则，如果任何付款人 Ai 的转账被判断为超时或被验证为失败，则合约将等值金额 A[i] 的押金退还给 C1 和 C2。中介C2最终根据收到的消息将coin2转给每个收款人B1、B2、B3……Bn。否则，如果向收款人 Bi 的转账超时或判定失败，则合约将向 Bi 发送等量的中介 C2 的保证金。最后，合约也会将中介C1剩余的t笔押金发送给C2。

// 算法2
输入：
	付款人账户地址：A1,A2,A3......An; 
	收款人：B1、B2、B3……Bn;
	中介：C1、C2; 
	总交易金额：t; 
	付款人Ai发送的金额：amountA[i];
	收款人Bi应收到的金额：amountB[i]; 
	时间阈值 T;
	
set 数组 amountB 中的每个元素 = 0；

if 中间人 C1 和 C2 都存入了 Ether
then
	所有付款人 A1,A2 ,A3 ......向中介 C1 转账 coin1;
	
	for i = 1 to n do
		if 付款人Ai转账成功 then
			记录 Ai;
			将Ai值amount_A[i]加到的收款人Bj对应的数组元素amount_B[j]中;
		else if 超时或确认失败 then
			t = t − amountA[i]; 
			将等同于amountA[i]的押金转移到C1和C2;
		end
	end
	
	中介C2将coin2分别转给收款人B1,B2......Bn;
	for i = 1 to n do
		if The transfer to Bi is successful then
			Record Bi;
			将等同于amountB[i]的C2押金将退还给C2;
		else if Timeout or confirmation fails then
			将等同于amountB[i]的C2押金转移到Bi;
		end
	end

	将中介C1的剩余数量为t的存款转移到C2;
	
else if C1 或 C2 没有在时间 T 内提供存款 then
	Return the deposit to C1 or C2 then terminate;
end

D. 交易验证阶段

中介C1和A之间的转移以及中介C2和B之间的转移有待确认。并且需要将验证结果发送到合约进行下一步。我们不能简单地要求任何用户参与交易验证，因为恶意用户可能会伪装成交易双方。例如，付款人可能会在没有任何实际转账的情况下向合同发送有关成功转账的欺诈性消息。同理，收款人收到货币后可能会发送转账失败的消息。在交易验证阶段，我们设计了一种可靠的方法，通过分散交易验证的权限来解决这个问题。

我们认为系统中有大量的中介，但每个交易进程只需要其中的两个。因此，其余的中间节点可以在我们的方案中用作验证器来验证交易。中介通过参与验证过程赚取费用。我们还要求每个节点在成为中介之前至少参与一次成功的验证过程。我们假设每个中介都有能力通过钱包、区块浏览器和许多其他工具来验证不同类型的加密货币的转移。一般来说，不同类型的加密货币都有自己的确认政策。例如，在比特币中，接收者假设他们的交易是安全的，附加了 6 个区块。

为了防止恶意用户注册多个中介账户来攻击验证过程，我们使用工作量证明（PoW）算法来确定参与验证委员会的中介集。操作由委员会合约完成，算法如算法3所示。

// 算法3
输入：
    节点账户: acc;
    随机数: nonce； 
    上个hash值: before;
    存款价值: value;

初始化：
    PoW难度：targer;
    最小存款：deposit_value;
    当前区块哈希：hash_now; 
    上次共识时间：time_last; 
    账户到委员会成员的Map：isMembers;
    当前委员地址Array：committee_member[w];
    委员人数：w;

if value ≥ deposit_value && before == hash_now then
	Record the current moment: now;
	Calculate the hash based on user input:
	h = hash(hash_now||nonce||acc)

	if target ≥ h && isMembers [acc] ==  false then
		target = target ∗ 10min / (now−time_last);
		time_last = now;
		isMembers[acc] = true;
		hash_now= h;
		
		if Size of array committeemember is equal to w then
			isMembers[committeemember[0]] = false 
			Erase committeemember[0]
		end

		Add acc to the last part of committee_member;
		
	else
		Termination;
	end
else
	Termination;
end

在加入验证委员会之前，受存款证明的启发，每个成功解决工作量证明难题的中介都需要支付一些以太币作为保证金。工作量证明难题要求节点根据前一个区块的哈希值和自己的以太坊账户选择一个随机数，使哈希结果小于目标值。我们设置了工作量证明难题的难度，使得参与委员会的两个中间人中的每一个都需要大约 10 分钟的时间来解决。这样，所有在 10 分钟内产生的交易都将由该委员会的中介进行验证。我们设置委员人数为w，要求同一个账号不能两次加入委员会。如果一个中间节点总是诚实的，它不仅会取回自己的押金，还会从不诚实节点的惩罚中获得奖励，从交易的担保中获得交易费用。因此，作为我们系统中的中间节点是有利可图的。交易验证委员会的构成如图 2 所示。

图2：交易验证委员会构成

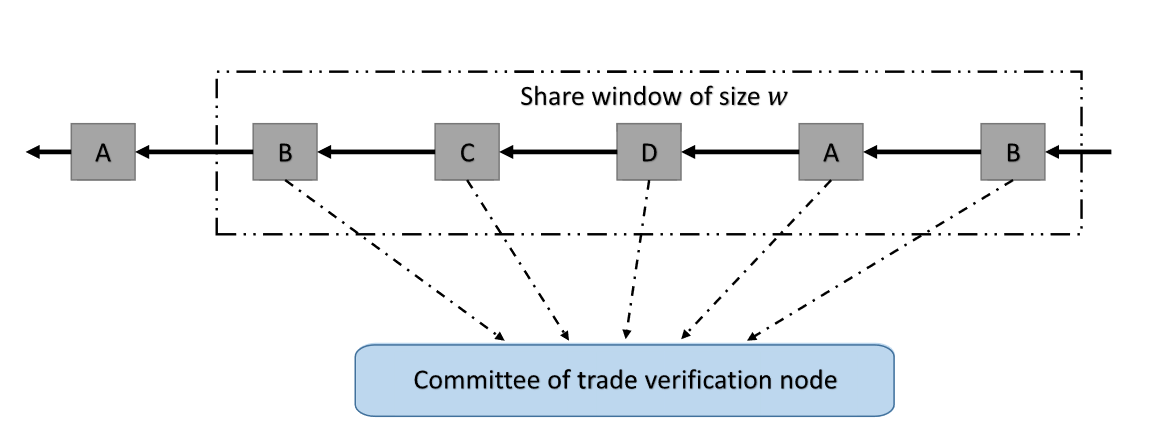
在每笔交易之后，验证委员会中的每个节点都需要验证交易并将自己的验证结果发送到智能合约。智能合约记录这些节点的地址并统计验证结果。然后，验证委员会将对给出冲突验证结果的节点进行分类。我们使用多数规则来确定最终的验证结果。为此，结果与最终结果冲突的节点将被视为不诚实，从而被排除在验证委员会之外。他们的存款将平均分配给诚实的节点。正确的结果将作为下一步的基础
的智能合约。对于验证委员会的规模，我们有一个 w 的数量限制。通过强制执行委员会规模，所有中间人的押金都会保留在合约中，直到任何不诚实的节点被排除在验证委员会之外。与计时策略类似，符合委员会规模允许在触发节点排除后将不诚实节点的存款转移到诚实节点。

VI. 安全分析

在本章中，我们将对我们的方案进行安全分析，并讨论我们的方案如何减轻或消除一些众所周知的针对区块链的攻击。

A. 去中心化和不可否认性

我们的方案完全不需要任何可信第三方的参与，而是通过智能合约和验证委员会以完全分布式的方式保证交易安全。参与协议的中介和验证委员会是通过完全分布式的安全策略来选择的。

在我们的方案中，除了付款人和收款人之外，其他涉及的实体仅包括中介和验证委员会，两者都不是中心化设计。首先，我们方案中需要的两个中介是从众多中介中挑选出来的。攻击者很难提前预测用户将选择和攻击的中介。只要有足够多的中介参与，我们的系统就不会退回到伪中心化系统。另一方面，验证委员会也在一定时间内解决了 PoW 问题的分布式节点中选出。委员会成员会随着时间的推移而变化，委员会成员的可靠性由PoW和保证金保证。因此，我们的协议既不依赖于任何中心化系统，也不回退到伪中心化系统。

而我们的方案也实现了转账执行后的不可否认性。这是因为一旦任何参与者发送或接收交易，该交易将通过智能合约存储在区块链中，不可篡改。并且有一个验证委员会来确保智能合约之外的区块链验证的安全性，因此任何参与者都不能否认自己的行为。

B. 可移植性

在我们的跨链加密货币交易方案中，我们支持多种类型的加密货币之间的交易。对于以太坊以外的其他加密货币的交易，我们都采用V-D节所述的方法，通过选择验证委员会来验证交易并将验证结果提供给合约。在协议的验证阶段，验证委员会中可能存在恶意节点，他们可能会提供错误的验证结果来干扰我们协议的执行。

在我们的方案中，验证委员会是通过工作量证明选择的，并要求用户提供足够的押金。而在我们的方案中，这两部分是不可或缺的。一方面，PoW 用于在一段时间内动态选择节点参与验证委员会。如果我们的方案设计为仅依赖于基于存款数量的绝对参与验证委员会的能力，那么用户可以轻松地将其存款分配到不同的账户来参与验证委员会，以及用户在验证委员会中的比例委员会仅与用户的存款有关。这样，拥有大量存款的用户会随着时间的推移积累更多的财富。一旦这种趋势持续下去，使得用户的财富积累足够，仅仅依靠存款证明并不能阻止用户完全掌握验证委员会的共识结果。同时，也没有任何有效的机制来阻止拥有足够存款账户的用户参与验证委员会。因此，我们还引入了工作量证明机制，该机制要求每时每刻只有计算出相应工作量证明谜题的节点才能参与验证委员会。它不仅保证了我们选择的验证委员会成员依赖于他们拥有的存款数量，而且还防止了权益的积累。它还可以防止具有大量存款的节点控制共识结果。

另一方面，如果我们这里只用工作量证明来做判断，普通用户也没有动力加入验证委员会，正确报告验证结果。即使报告了错误的结果，用户也不会受到任何惩罚，只能被踢出委员会。验证委员会中的每个用户都需要提供押金，作为对报告正确验证结果的诚实用户的奖励，以及对报告错误验证结果的恶意用户的惩罚。恶意用户的押金也作为对正确举报用户的奖励，以激发其诚实行为。

我们假设对于想要加入验证委员会的节点，恶意节点的总算力在任何时候都应该小于总算力的 1/4。否则，就会出现自私挖矿攻击[44]。假设总共选择了 w个节点加入验证委员会。如果我们要求来自多数规则的最终验证结果的计数超过 a，则意味着验证委员会中恶意节点的百分比被强制要求小于 $t = (w-a) / w$ 。我们假设 X 是一个随机变量，代表我们在验证委员会中选择拜占庭节点的次数。这样，恶意节点的最大数量 c 等于 $w\times{t}$ 。我们可以使用累积二项分布来计算w节点委员会中恶意节点比例小于t时的概率P[45]。

P[X\leq c]=\sum_{k=0}^{c}{\binom{w}{k}p^k(1-p)^{w-k}}

表III第一列表示委员会中恶意节点的比例不超过t，第一行代表委员会中的节点数。数据表明，在确定验证委员会的节点数时，恶意节点的比例不超过t的概率。当委员会中的恶意节点数量不超过 t 时，恶意节点提供的错误验证结果的比例不会超过 t，因为正常节点肯定会提供正确的验证结果。这样，一旦合约收集的验证结果超过t的比例，就可以将结果视为最终的正确结果。例如，当我们取 10 个验证委员会成员时，恶意节点的数量不超过总数的 1/2 的概率为 0.99。这意味着，如果智能合约得到半数以上的验证委员会成员一致的判断，当恶意节点的比例不超过 1/2 时，就可以认为这个结果是正确的。由于正常节点肯定会提供正确的验证结果，因此合约收集到的错误验证结果不会超过委员会中恶意节点数量的比例。从表中也可以看出，验证委员会的成员人数越多，合约在收集到足够多的验证后得到正确判断结果的概率就越大。然而，即使验证委员会的成员数量很少，该方案在我们的假设中仍然是安全的。

表III：拜占庭节点在所有委员会成员中的比例的二项分布（BINOMIAL DISTRIBUTION）

t/w	10	20	50	100
0.7	0.9997	1.0000	1.0000	1.0000
0.6	0.9965	1.0000	1.0000	1.0000
0.5	0.9957	0.9992	1.0000	1.0000
0.4	0.9219	0.9784	0.9937	0.9997
0.3	0.7759	0.8034	0.8369	0.8962

C. 公平性

如第 V-C.1 节和第 V-C.2 节所述，在我们的协议过程中，无论 C1 或 C2 未能在规定时间内提供押金，或付款人的转账超时或失败，合约都将退还C1 或 C2 并终止协议。因此，诚实行为的参与者在这个过程中不会有任何损失。我们不能保证中介被选中后是完全可靠的，但可以保证即使中介出现恶意行为，也不会对跨链交易双方造成任何损失。

一方面，对于中介C1来说，他/她唯一能做的恶意行为就是在获得A的转账后，假装转账失败，从而终止合约，获得A的转账。但是在我们的协议中，A 和 C1 之间的转账交易的验证结果是由验证委员会来保证的。一旦C1提供了与A交易的保证金和账户地址，他/她的行为就完全受合约控制。如果合约从验证委员会收到转账成功的验证结果，将自动执行后续操作。否则，如果转账结果失败或超出定时器范围，合约将退还两个中介的押金并终止操作。

另一方面，如果C1是诚实的，而C2是恶意的，没有转给B，合约就会把C2的押金转给B。因为我们要求无论是C1还是C2，合约中的实际押金金额不小于 A 和 B 实际转移的金额。因此，在将 C2 的存款转给 B 后，B 也可以使用这笔存款通过我们的方案兑换他/她需要的加密货币。在这种情况下，A 已成功将加密货币转移到 C1。因此，为了防止 A 在这个过程中获得额外的加密货币，我们选择将 C1 的存款发送给 C2。这样，A就完成了正常的计划流程，并没有损失任何收益。总的来说，我们的跨币种交易方案已经针对A和C1进行了成功。对于 C2，智能合约中记录了异常交易。但是对于Bit来说，完成从存款到他/她需要的其他类型货币的转换是必要的。与正常流程相比，这确实带来了额外的开销。但是可以保证程序正常进行。如果该计划终止，将带来不低于现有计划的成本。由于 A 转给 C1 的加密货币不再退还，我们不能仅通过结束程序来保证安全。一种可能的解决方案是将 C1 的押金退还给 A，但这也会带来不少于我们现有解决方案的额外开销。

D. 稳定性

在第 IV-B 节中描述的安全假设下，我们的协议可以很好地抵御区块链网络中的常见攻击。

1）Double-Spend Attack：在我们的方案中，存在付款人委托两个不同的中介同时向不同用户进行相同支付的情况。或者在委托中介过程中，付款人可以在其他场合进行同样的付款。为了防止双花攻击[46]，我们的方案要求验证者遵守加密货币本身的验证方法。例如，如果付款人以比特币支付，则验证者必须在交易后等待 6 个以上的区块才能将其判断发送到合约。我们的方案不会对所涉及的加密货币进行任何更改，以确保加密货币交易的安全性。

2）女巫攻击Sybil Attack：任何用户都可以发送交易请求，即使用户在向合约发送应用程序后没有进行后续转账。在这种情况下，只会损失少量的以太坊交易费用。在此过程中，恶意用户可能会发送大量的小额交易请求，甚至可能会在请求发出后拒绝发起交易。但是，在我们的方案中，允许中介在收到用户的交易请求后进行选择。也就是说，中介可以通过用户的账户地址来确认账户有足够的余额。如果转账金额太小，中介将移除用户请求，从而确保用户不是 Sybil 节点 [47]。

3）DoS 攻击：恶意节点可能会伪造大量账号试图加入验证委员会或冒充中间人，通过 DoS 攻击破坏正常的协议进程。但是，我们的方案不会受到这些恶意行为的影响，因为我们有两个预防措施。首先，验证委员会的每个成员都应该支付一些以太币作为保证金。其次，每个节点都需要提交 PoW 难题的解决方案，才能被认可为验证委员会的成员。因此，恶意节点无法轻易伪造身份加入验证委员会而无需支付任何费用。同样，恶意节点也不能充当中介，因为中介节点需要有加入验证委员会的记录。

E. 原子性

交易的原子性要求跨链交易必须要么完全成功要么完全失败。在我们的方案中，不会出现一方付款而另一方没有收到转账的情况。我们的方案通过基于智能合约和超时判断的协议设计来实现这一目标。

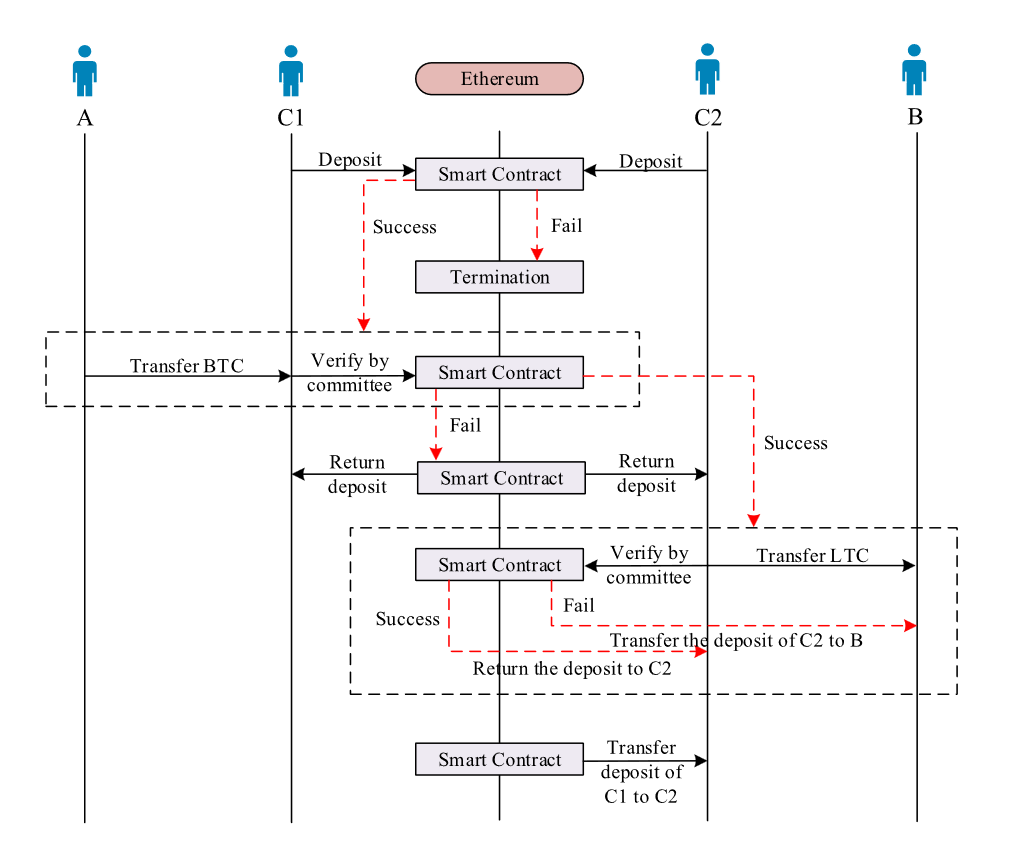
在我们的方案中，如果所有参与者都正常遵守协议，交易将被正确执行。如果一些联盟偏离了协议，在正常执行中不会对参与者造成任何损失。并且协议将被终止或违反操作将受到惩罚。如图 3 所示，我们的协议具有三个执行判断。第一个是中介需要在开始时提供足够的押金，并在智能合约上设置哈希时间锁。然后，A 可以转移到 C1。这里我们依靠验证委员会来判断交易结果，并在合约中设置时间锁定，以防止转账超时。如果传输失败，则交易终止。最后，需要中介C2向B转账，验证委员会也验证交易结果并设置哈希时间锁，防止转账超时。如果C2恶意不转账给B，合约会将C2的保证金转账给B，因此B会收到不少于他/她到期价值的转账货币。在这种情况下，遵守协议的一方不会遭受损失，恶意方也不会从中获得任何好处。因此，恶意方没有动机偏离我们的协议。

图3：协议状态转移图

F. 安全性和活力

安全性：诚实（非拜占庭）节点同意相同的值。

证明：如果所有诚实节点都同意交易验证的相同结果，则提议的协议提供安全性。
为了实现这一点，利用多数规则来确定最终的验证结果。对于要验证的交易 tx，每个验证节点 Pi 将给出以下两个结果之一： Validation(tx, Pi ) = true 或 Validation(tx, Pi) = false 。冲突的验证结果将验证节点分为两组：True(tx) = { Pi, Validation(tx, Pi ) = true} 和 False( tx) = { Pj , Validation(tx, Pj ) = false }。通过使用多数规则，如果|True(tx)|>|False(tx)|，则最终验证结果为真；否则，即如果 |False(tx)|>|True(tx)|，它将为 false 。根据我们的安全假设，委员会中拜占庭节点的数量少于 1/4，给出最终验证结果的节点是诚实的，其他的都是拜占庭节点。我们选择通过反证法来证明这个特征。我们要表明，根据多数规则，委员会不可能同时承认真假。对于最终结果为真的认可，必须是委员会中半数以上的节点都认可了“真”。同时，对于最终结果为false的认可，必须是“false”也得到了委员会半数以上节点的认可。然而，这意味着 ||True(tx)| + |False(tx)||大于委员会成员总数，这是不可能的。因此，这就产生了矛盾，因为这两个结果都不能同时被委员会中超过一半的节点认可。换句话说，诚实节点不同意这两种不同的结果，从而证明我们的协议实现了安全性。

活力：事务最终会中止或提交。

证明：在我们的方案中，我们采用弱同步/部分同步的时间假设，这意味着保证消息在一定的时间限制后被传递。我们方案的设计也是基于这个假设。因此，我们的方案将在智能合约中设置一个计时器，以防止恶意节点拒绝提供验证结果。在这种弱/部分同步时间假设下，按照执行顺序，合约中有五种请求：R1（C1&C2存款）、R2（付款人转账）、R3（付款人确认）、R4（收款人转账）和R5 （收款人确认）。因此，有六个有效状态：S0（开始）、S1（中介存款）、S2（付款人转移）、S3（付款人确认）、S4（收款人转移）、S5（收款人确认）。在每个状态 Si ，合约等待相应的请求 Ri+1。如果成功，则合约转移到下一个状态 Si+1；否则，如果失败或超时，则合约终止并宣布交易失败。如果合约成功遍历了有效的状态转换序列，即“S0→R1→S1→R2→S2→R3→S3→R4→S4→R5→S5”，则交易成功完成。总之，合约总是在进步，永远不会在任何状态下无限期地阻塞。因此，我们的协议实现了活力。

VII 性能分析

为了评估我们方案的部署成本，我们在以太坊的官方测试网络 Ropsten [48] 上部署了我们的合约。 Gas 用于衡量智能合约代码中每一步的成本。表 IV 中概述了第 V-B 部分中描述的每个功能的 Gas 和财务成本。我们使用 1 以太币 = 130 美元的兑换率和 0.000000003 以太币的gas价格（即 2020 年 4 月的实际成本）估算了以美元（美元）为单位的成本。中间人计算 PoW 难题的代码未包含在合约，因为用户可以在他们的本地机器上执行这部分并将结果发送到合约。

表IV：每个操作所花费Gas值

Transaction	Gas	USD
IC.Deploy	3,690,283	1.43
IC.Register	181,591	0.07
IC.Update	80,995	0.03
CC.Verify_PoW	191,737	0.07
TC.Prepare	398,525	0.15
TC.Deposit	36,452	0.01
TC.Validation	163,780	0.06

对于需要进行跨币种交易的用户，只需要用户调用TC.Prepare的功能即可。即使是多方情况，每个用户也只需要调用一次该函数，费用为 0.15 美元。对于中级用户，有 IC.Register 和 IC.Update功能提供自己的信息，分别只需 0.07 美元和 0.03 美元。在一笔交易中，为每个中介发行存款的操作平均成本为 0.01 美元。想要加入验证组的中介需要执行 CC.Verify_PoW 的验证操作，费用为 0.07 美元。验证的费用由验证组的每个成员承担。根据我们合约的调用开销，用户可以选择是否在可接受的范围内使用我们的服务

A. 时序分析

我们还测量了合约的运行时间。所有测量均在运行 Windows 10、配备 6 核、3.0 GHz Intel Core i5 和 8 GB DDR4 RAM 的台式机上进行。在本节中，我们将展示我们方案的运行时结果，这表明我们的合约可以在可接受的时间开销内实现预期的功能。

我们方案的实现分为两部分：链下部分和链上部分。用户加入验证组执行的 PoW 拼图计算在用户本地机器上进行链下。智能合约只需要通过IC.Verify_PoW函数接收和验证PoW谜题的解法，并根据解题时间调整PoW的难度值。这样，解决PoW问题的时间间隔可以保持在十分钟左右。对于链上部分，我们只考虑方案中智能合约的运行时间。该方案涉及其区块链上其他类型加密货币的确认时间，我们不考虑。

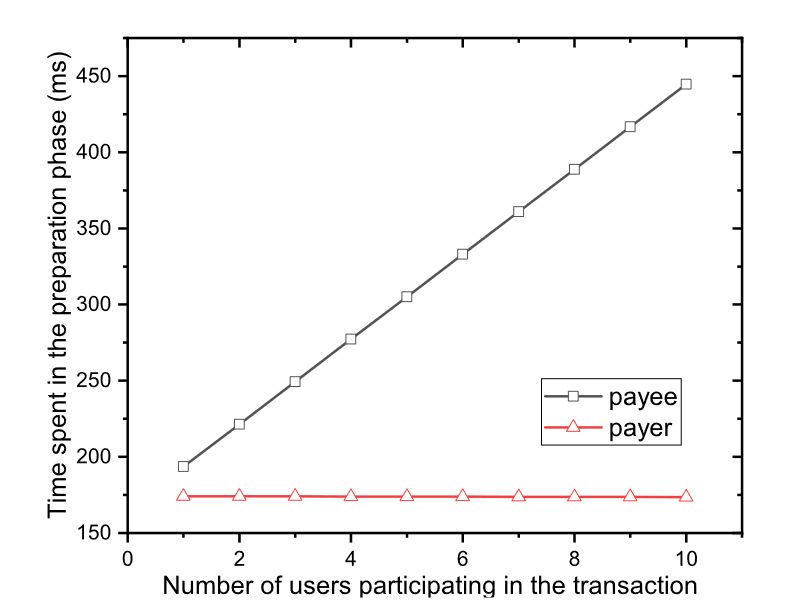
由于gas和区块大小的限制，我们在一轮协议过程中将参与交易的付款人和收款人的数量设置为少于10个。当我们改变参与交易的用户数量时，主要影响合约准备阶段的执行时间。我们记录了通过 TC.Prepare 函数独立调用合约的用户的最大执行时间，结果如图 4 所示。我们可以看到，我们的合约运行时间随着收款人数量的增加而增加。这是因为对于单个付款人，合约需要记录和处理用户的每个收款人的信息。因此，所有收款人的数量越多，发送到合约的信息就越多，从而导致合约的整体运行时间更长。也可以看出，由于每个支付者都是不同的节点，他们的操作是并行的。增加付款人的数量不会显着增加合约运行时间。因此，合约的准备时间仅受每个付款人的交易用户数量影响。在收集到十个用户的请求或超过此等待时间后，合约将进行下一步。

图4：当收款人数量增加时，在准备阶段花费的时间

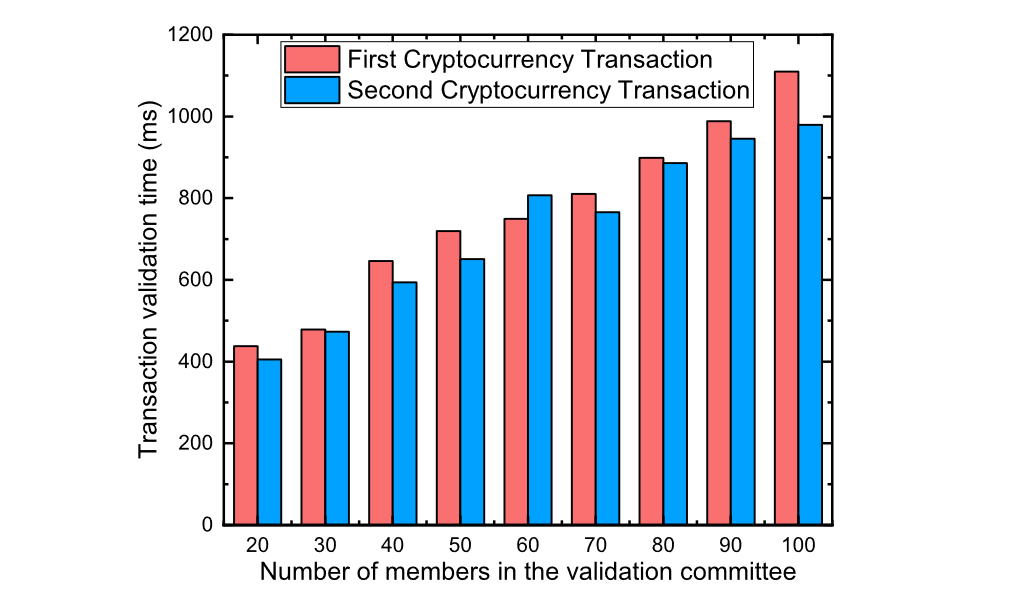
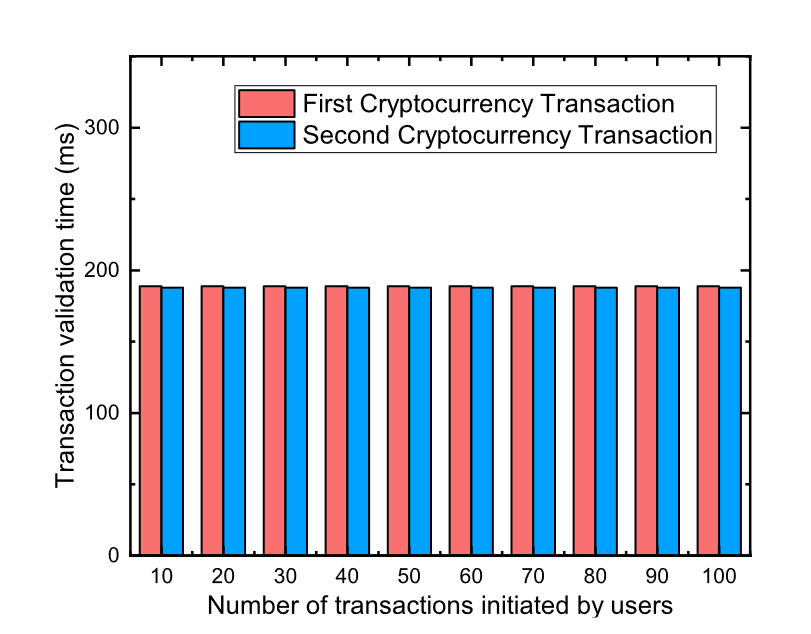
我们还改变了验证委员会的用户数量和一对用户之间的交易数量，以分析合约在验证过程中的表现。当我们改变验证委员会的参与者数量时，合约通过 TC.Validation 函数执行这一步所需的时间如图 5 所示。第一个验证是针对付款人与中介 C1 之间的交易，而第二个验证用于中介 C2 和收款人之间的交易。我们可以看到，当验证委员会成员数量增加时，验证过程所需的时间也会显着增加。尽管如此，即使验证委员会有 100 名成员，每个验证过程也只需要大约 1 秒钟。与确认比特币等公共区块链加密货币交易所需的时间相比，这个时间可以忽略不计。我们也可以从图 6 中看出，随着付款人和单个收款人之间的交易数量增加，不会增加通过合约进行交易验证的时间成本。这是因为同一对用户之间的所有交易都会通过合约合并为一笔交易，从而不会增加时间成本。

图5：当验证委员会规模增加时，在验证阶段花费的时间

图5：当一对用户之间的交易数量发生变化时，验证阶段花费的时间。

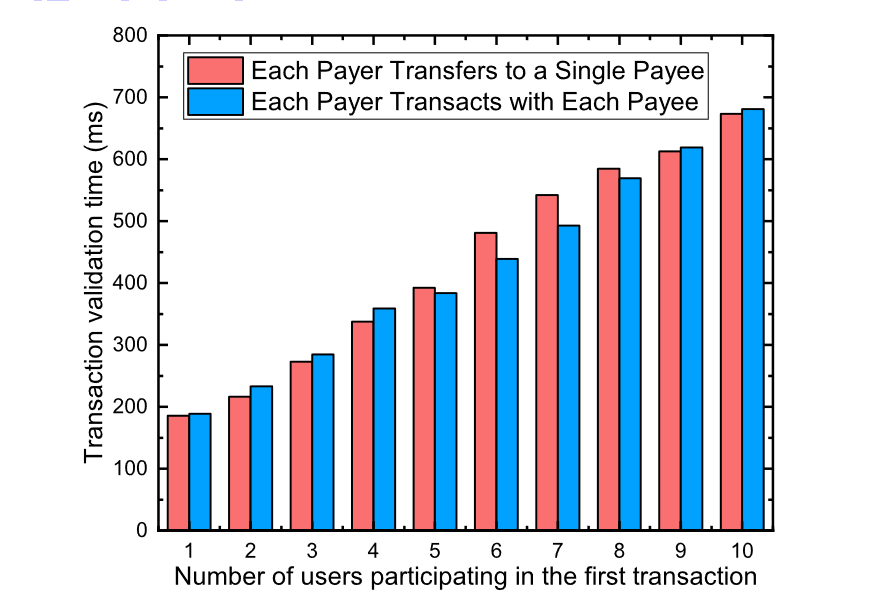
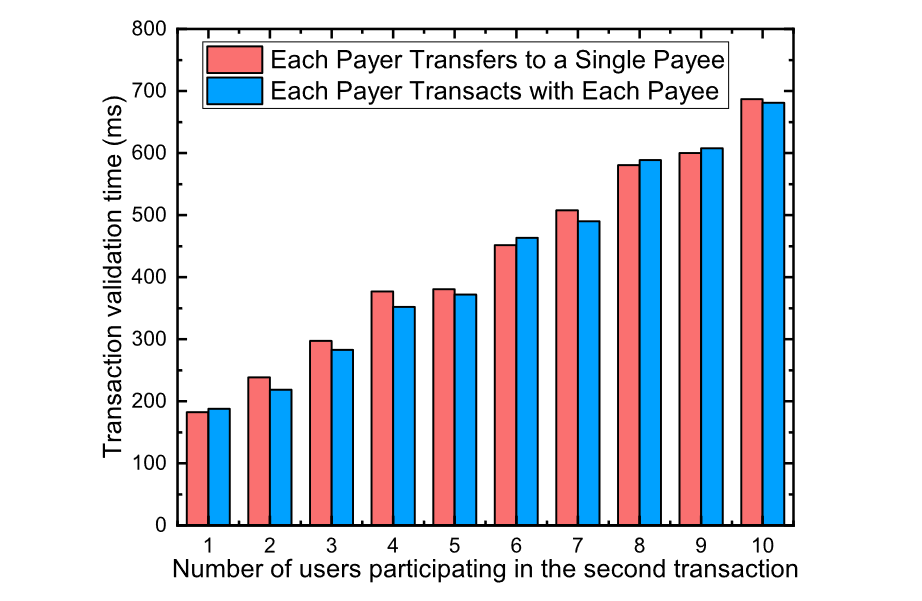
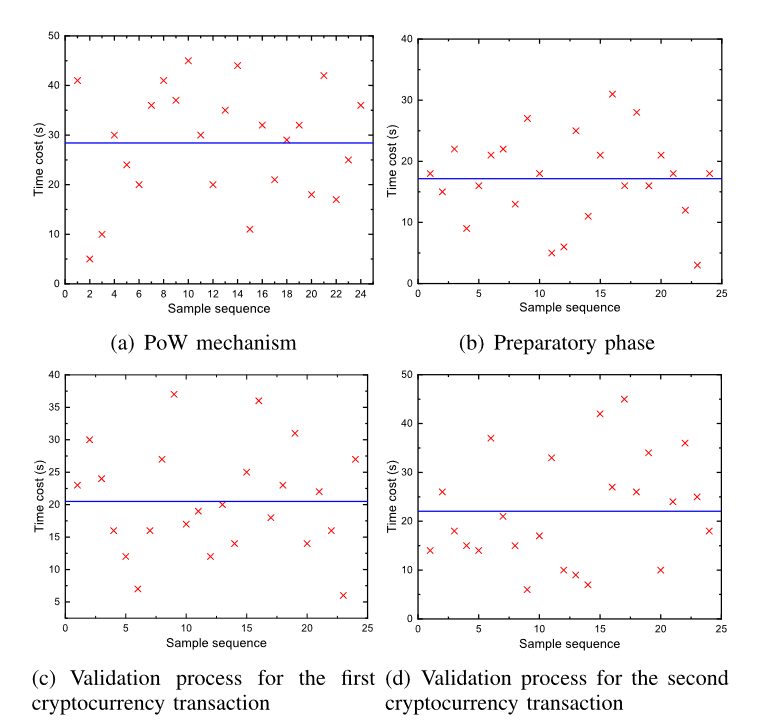
当我们增加参与交易的用户数量时，每个额外用户的每笔额外交易都会增加合约的运行成本。为了实验的方便，我们同时添加了一对payer和payee。图 7 和图 8 分别显示了两个交易所需的验证时间。两个图中的两个彩色列代表两种不同的情况。第一种情况是每个付款人都与一个收款人进行交易，其中交易的数量等于参与者的数量。而第二种情况是每个付款人与每个收款人进行交易，其中交易数量是参与者数量的两倍。但是，在允许误差范围内，我们可以从图中得出结论，两种情况下的时间成本是相同的。这意味着我们方案的验证时间仅受参与交易的用户数量影响，而与每个用户的交易数量无关。这是因为在我们的合约中，每个参与用户所涉及的交易都是合并的，这也是我们的解决方案在大量交易的情况下保持高吞吐量的前提。

图7：第一次加密货币交易的验证过程所花费的时间

图8：第二次加密货币交易的验证过程所花费的时间。

我们还测量了在不同时间调用合约主要功能所需的验证时间。如图 9 所示，虽然测试链上的验证时间只能作为参考，但可以看出合约执行时间与交易确认时间相比可以忽略不计。因此，我们的解决方案所需的机器上的执行时间是可以接受的。在未来的工作中，我们还将把我们的合约部署在以太坊主链上，以便在实际网络下进行测试。

图9：协议主要步骤中交易验证的时间成本（a. 工作证明机制；b. 预备阶段；c. 第一次加密货币交易验证过程；d. 第二次加密货币交易验证过程）

VIII 结论

在本文中，我们提出了一种基于智能合约的多用户交易的去中心化跨加密货币交换方案。在我们的方案中，我们使用以太作为连接不同类型加密货币之间的交易的传输方式。我们还实现了合约并评估了它在本地机器上的执行开销。结果表明，我们方案的时间成本仅受参与交易的用户总数的影响，而用户交易的数量对我们合约的运行时间没有显着影响。

未来，我们将从两个方面从实验部分进一步完善我们的方案。
首先，我们会争取更多的参与者来完成该计划的实施。其次，我们将在以太坊主网上部署我们的方案，以测试我们的方案在实际网络中的成本

引用

The authors sincerely thank the Editor, Dr. Debdeep Mukhopadhyay, and the anonymous referees
for their valuable suggestions that have led to the present improved version of the original manuscript.

[1] S. Nakamoto. Bitcoin: A Peer-to-Peer Electronic Cash System. 2008.
Accessed: Apr. 2021. [Online]. Available: https://bitcoin.org/bitcoin.pdf

[2] C. Lee. (2011). Litecoin. Accessed: Apr. 2021. [Online]. Available:
https://litecoin.org/

[3] G. Wood. (2017). Ethereum: A Secure Decentralised Generalised Trans-
action Ledger EIP-150 REVISION (759dccd-2017-08-07), Ethereum
Project Yellow Paper. Accessed: Apr. 2021. [Online]. Available:
https://ethereum.github.io/yellowpaper/paper.pdf

[4] P2PB2B. Accessed: Apr. 2021. [Online]. Available: https://p2pb2b.io

[5] MXC. Accessed: Apr. 2021. [Online]. Available: https://mxc-exchange.
zendesk.com/hc/zh-cn

[6] BKEX. Accessed: Apr. 2021. [Online]. Available: https://www.bkex.co

[7] Bilaxy. Accessed: Apr. 2021. [Online]. Available: https://bilaxy.com

[8] LBank. Accessed: Apr. 2021. [Online]. Available: https://www.lbank.
info

[9] C. Y. Kim and K. Lee, “Risk management to cryptocurrency
exchange and investors guidelines to prevent potential threats,” in
Proc. Int. Conf. Platform Technol. Service (PlatCon), Jan. 2018,
pp. 1–6.

[10] R. Khalil, A. Gervais, and G. Felley. (2019). TEX-A Securely Scalable
Trustless Exchange, Cryptology ePrint Archive. [Online]. Available:
https://eprint.iacr.org/2019/265

[11] E. Heilman, S. Lipmann, and S. Goldberg, “The Arwen trading proto-
cols,” in Proc. Int. Conf. Financial Cryptogr. Data Secur. (FC). Berlin,
Germany: Springer, 2020, pp. 156–173.

[12] L. Luu, D.-H. Chu, H. Olickel, P. Saxena, and A. Hobor, “Making smart
contracts smarter,” in Proc. ACM SIGSAC Conf. Comput. Commun.
Secur. (CCS), 2016, pp. 254–269.

[13] V. Buterin. (2014). A Next-Generation Smart Contract and Decentralized
Application Platform. Accessed: Apr. 2021. [Online]. Available: https://
cryptorating.eu/whitepapers/Ethereum/Ethereum_white_paper.pdf

[14] Metronome. Accessed: Apr. 2021. [Online]. Available: https://www.
metronome.io

[15] Y. V. L. Luu. (2018). Kybernetwork: A Trustless Decentralized Exchange
and Payment Service. Accessed: Apr. 2021. [Online]. Available:
https://whitepaper.io/document/43/kyber-network-whitepaper

[16] J. Chow. BTC Relay. Accessed: Apr. 2021. [Online]. Available: https://
github.com/ethereum/btcrelay

[17] F. Vogelsteller and V. Buterin. (2015). EIP 20: ERC-20 Token Stan-
dard. Accessed: Apr. 2021. [Online]. Available: https://eips.ethereum.
org/EIPS/eip-20

[18] W. Warren and A. Bandeali. (2017). 0x: An Open Protocol for Decen-
tralized Exchange on the Ethereum Blockchain. Accessed: Apr. 2021.
[Online]. Available: https://github.com/0xProject/whitepaper

[19] EtherDelta. Accessed: Apr. 2021. [Online]. Available: https://etherdelta.
com

[20] IDEX. Accessed: Apr. 2021. [Online]. Available: https://idex.market

[21] (2019). TBTC: A Decentralized Redeemable BTC-Backed ERC-20
Token. Accessed: Apr. 2021. [Online]. Available: https://docs.keep.
network/tbtc/index.pdf
[22] T. Zhang and L. Wang. (2017). Republic Protocol. Accessed: Apr. 2021.
[Online]. Available: https://republicprotocol.github.io/whitepaper/
republic-whitepaper.pdf

[23] J. Teutsch, M. Straka, and D. Boneh, “Retrofitting a two-way peg
between blockchains,” 2019, arXiv:1908.03999. [Online]. Available:
http://arxiv.org/abs/1908.03999

[24] J. Kwon and E. Buchman. (2016). Cosmos: A Network of Distrib-
uted Ledgers. Accessed: Apr. 2021. [Online]. Available: https://cosmos.
network/whitepaper

[25] G. Wood. (2016). Polkadot: Vision for a Heterogeneous Multi-
Chain Framework. Accessed: Apr. 2021. [Online]. Available: https://
github.com/w3f/polkadot-white-paper/raw/master/PolkaDotPaper.pdf

[26] J. Kwon. (2014). Tendermint: Consensus Without Mining, Draft
V.0.6. Accessed: Apr. 2021. [Online]. Available: https://tendermint.
com/docs/tendermint.pdf

[27] A. Zamyatin, D. Harz, J. Lind, P. Panayiotou, A. Gervais, and
W. Knottenbelt, “XCLAIM: Trustless, interoperable, cryptocurrency-
backed assets,” in Proc. IEEE Symp. Secur. Privacy (S&P), May 2019,
pp. 193–210.

[28] I. Bentov, Y. Ji, F. Zhang, L. Breidenbach, P. Daian, and A. Juels,
“Tesseract: Real-time cryptocurrency exchange using trusted hardware,”
in Proc. ACM SIGSAC Conf. Comput. Commun. Secur. (CCS), 2019,
pp. 1521–1538.

[29] S. Matetic, M. Ahmed, K. Kostiainen, A. Dhar, D. Sommer, and
A. Gervais, “ROTE: Rollback protection for trusted execution,” in Proc.
26th USENIX Secur. Symp. (USENIX Security), 2017, pp. 1289–1306.

[30] N. Weichbrodt, A. Kurmus, P. Pietzuch, and R. Kapitza, “AsyncShock:
Exploiting synchronisation bugs in intel SGX enclaves,” in Proc. Eur.
Symp. Res. Comput. Secur. (ESORICS). Berlin, Germany: Springer,
2016, pp. 440–457.

[31] M. Herlihy, “Atomic cross-chain swaps,” in Proc. ACM Symp. Princ.
Distrib. Comput. (PODC), 2018, pp. 245–254.

[32] M. Herlihy, B. Liskov, and L. Shrira, “Cross-chain deals and adversarial
commerce,” Proc. VLDB Endowment, vol. 13, no. 2, pp. 100–113, 2019.

[33] G. Malavolta, P. Moreno-Sanchez, C. Schneidewind, A. Kate, and
M. Maffei, “Anonymous multi-hop locks for blockchain scalability
and interoperability,” in Proc. Annu. Netw. Distrib. Syst. Secur. Symp.
(NDSS), 2019, pp. 1–15.

[34] E. Tairi, P. Moreno-Sanchez, and M. Maffei (2019). A2L: Anony-
mous Atomic Locks for Scalability and Interoperability in Pay-
ment Channel Hubs, Cryptology ePrint Archive. [Online]. Available:
https://eprint.iacr.org/2019/589.pdf

[35] P. Moreno-Sanchez, A. Blue, D. V. Le, S. Noether, B. Goodell, and
A. Kate, “DLSAG: Non-interactive refund transactions for interoperable
payment channels in Monero,” in Proc. Int. Conf. Financial Cryptogr.
Data Secur. (FC), 2019, pp. 325–345.

[36] C. Egger, P. Moreno-Sanchez, and M. Maffei, “Atomic multi-channel
updates with constant collateral in Bitcoin-compatible payment-channel
networks,” in Proc. ACM SIGSAC Conf. Comput. Commun. Secur.
(CCS), 2019, pp. 801–815.

[37] S. King and S. Nadal. (2012). PPCoin: Peer-to-Peer Crypto-
Currency With Proof-of-Stake. Accessed: Apr. 2021. [Online]. Available:
https://peercoin.net/assets/paper/peercoin-paper.pdf
[38] (2018). EOS.IO Technical White Paper V2. Accessed: Apr. 2021.
[Online]. Available: https://github.com/EOSIO/Documentation/blob/
master/TechnicalWhitePaper.md

[39] Y. Sompolinsky and A. Zohar, “Secure high-rate transaction processing
in Bitcoin,” in Proc. Int. Conf. Financial Cryptogr. Data Secur. (FC).
Springer, 2015, pp. 507–527.

[40] M. Castro and B. Liskov, “Practical byzantine fault tolerance,” in Proc.
3rd Symp. Operating Syst. Design Implement. (OSDI), 1999, vol. 99,
no. 1999, pp. 173–186.

[41] M. Castro and B. Liskov, “Practical Byzantine fault tolerance and proac-
tive recovery,” ACM Trans. Comput. Syst., vol. 20, no. 4, pp. 398–461,
2002.

[42] D. Ongaro and J. K. Ousterhout, “In search of an understandable
consensus algorithm,” in Proc. USENIX Annu. Tech. Conf. (ATC), 2014,
pp. 305–319.

[43] A. Zamyatin et al. (2019). SoK: Communication Across Distrib-
uted Ledgers, IACR Cryptology ePrint Archive. [Online]. Available:
https://eprint.iacr.org/2019/1128.pdf

[44] I. Eyal and E. G. Sirer, “Majority is not enough: Bitcoin mining is
vulnerable,” in Proc. Int. Conf. Financial Cryptogr. Data Secur. (FC).
Berlin, Germany: Springer, 2014, pp. 436–454.

[45] E. K. Kogias, P. Jovanovic, N. Gailly, I. Khoffi, L. Gasser, and B. Ford,
“Enhancing Bitcoin security and performance with strong consistency

via collective signing,” in Proc. 25th USENIX Secur. Symp. (USENIX
Security), 2016, pp. 279–296.
[46] G. O. Karame, E. Androulaki, and S. Capkun, “Double-spending fast
payments in Bitcoin,” in Proc. ACM Conf. Comput. Commun. Secur.
(CCS), 2012, pp. 906–917.
[47] J. R. Douceur, “The Sybil attack,” in Proc. 1st Int. Workshop Peer-to-
Peer Syst. (IPTPS). Berlin, Germany: Springer, 2002, pp. 251–260.

[48] The Ethereum Block Explorer: ROPSTEN (Revival) TESTNET.
Accessed: Apr. 2021. [Online]. Available: https://ropsten.etherscan.io