Reading paper in FIT5152: 知识评估和进展分析与设计的统一框架 A Unified Framework for Knowledge Assessment and Progression Analysis and Design

发表于 2020-11-04 更新于 2021-10-11

作者 Shuhan Wang, Fang He & Erik Andersen

论文翻译，侵删

摘要

设计引人入胜的学习内容固然重要，但也很困难，并且通常涉及许多手动规范。我们提出了一个统一的框架，该框架利用自动问题分解和部分排序图的构建来简化多个工作流：知识评估以及进行性分析和设计。我们通过在线日语评估工具对847名参与者进行了研究，结果表明我们的框架可以有效地衡量学生的能力并预测学生在特定问题上的表现。我们还提供了对课程分析的结果，结果表明两种不同教科书的进度令人惊讶地相似，并且我们的框架可以导致发现专家进行设计的一般原理。最后，我们演示了自动进度生成以及所需的排序和步调，允许进行进度定制以及将从一个课程中提取的参数映射到另一个课程

ACM Classification Keywords

H.5.0 Information Interfaces and Presentation: General

Author Keywords

education; automatic problem decomposition; knowledgeassessment; progression analysis and design

简介

教育中的一个关键挑战是保持学生的参与度，而首要考虑的是向特定学生展示最佳知识的顺序。排序是一个挑战：首先应该引入哪些知识？另一个速度是：进步会变得越来越困难。尽管有教育和心理学等方面的指导原则[15，55，59]可以帮助设计进步，但缺乏务实和自动的方法来弥合教育理论与实践之间的差距，尤其是整个课程的规模。设计和优化进度的困难也限制了课程适应每个学生需求的能力

在HCI中，此问题与教育软件[7、14]，视频游戏[11、22、33、37、45]和软件可学习性[25、31]的设计有关。目前，我们主要是手工设计进度，这很昂贵，并且限制了我们寻找最佳进度的实验能力。最近，在自动进度设计中已有一些工作[6，11]。尽管这项工作能够自动组织内容，但仅解决了程序性主题和视频游戏级设计。我们仍然缺乏一个通用的框架来表征能够处理一些非过程性主题（如语言学习）的教育进程。此外，我们需要一种形式上的方法来使用相同的框架来评估学生的知识，以便我们可以针对该学生量身定制学习进度和进度。理想情况下，我们将能够在不费吹灰之力的情况下针对广泛的教育领域建立适应性的进步。

在本文中，我们提出了一个框架，该框架允许针对非过程性任务进行自动问题分解和部分排序图构造。该框架促进了多个工作流程。它建立在项目反应理论[53]，知识空间理论[28]和知识追踪[14]的基础之上，以创建学生知识和问题难度的多维度量，从而可以快速评估和预测绩效。它还定义了起搏和其他进度参数的参数空间，并提供了一种方法来表征和比较进度以及设计符合所需参数的新进度。

我们对框架进行了多次评估。首先，我们提出了对自动问题分解和偏序图构建的理论贡献，以帮助外语学习语法，这是一个重要的非程序性主题。然后，我们讨论了一个有847名参与者的用户对日语评估工具的评估，这表明我们的自动评估算法可以根据项目响应理论准确地进行能力评估和绩效预测。我们还提供了自动分析语言学习进度的结果，显示出两本用于学习日语的教科书令人惊讶地具有相似的节奏和其他进阶特征，并且两种在线语言学习工具具有非常不同的进阶设计策略。最后，我们证明了我们的框架可以自动生成具有所需特征的进度，例如学习进度以及学习和复习的比例。这使得从进度分析中获得的见解可以直接应用于进度设计和个人进度剪裁

非过程技能的部分排序

为了选择适合每个学生的难易程度的练习问题，我们需要一个层次结构来编码问题之间的难度关系。一种简单的方法是请专家指定这些关系。但是，随着问题集的规模越来越大，这变得异常困难。理想情况下，我们将具有自动组织问题的方法。

在先前的工作中[6，12]，研究人员为过程任务建立了部分排序图。这项工作使用过程执行跟踪来组织内容，并对这些跟踪进行部分排序以创建分层的内容结构。例如，一个人可以识别出解决整数加法问题所需的至少四个基本技能：不带进位的一位数字加法（A），不带进位的一位数字加法（B），写进位（C），然后放下最后一个进位（D）。例如，问题可以分解为以下基本技能

问题	2+3	15+18	93+15	298+865
追溯	A	ACB	AACD	ACBCBD

但是，在某些领域（例如语言学习）中，目标对象的知识无法轻松地建模为单个过程。要在此类领域引入层次化的知识结构，我们需要对过程领域进行泛化。为此，我们的框架利用了组合性这一概念，即可以将问题分解为较小的概念单元。在一些半程序领域，例如数学和语言学习中，对此进行了充分的研究[6，60]。

例如，日语句子可以分解为语法模板，专家语言教师和语言学家认为语法单元是最重要的语法知识，并让学生实际学习语言课程。这些模板已被证明对语言学习者的文本难度评估很有帮助[60]。我们发现，语法理解日语句子的特定任务可以分解为（多个）语法模板集。例如，这是三个日语句子及其语法模板

我们可以看到S1只有一个语法模板：（–の）。对于日语学习者来说，S2比S1更难，因为它不仅具有（–の）而且还有另一个模板（–は）。 S3重复相同的模板（–の）两次，因此也比S1难。这些关系无法通过[6]中的部分排序来捕获，因为尚不清楚如何程序化人类如何理解这些句子的过程。但是，通过考虑概念的多集而不是执行跟踪，我们可以按如下方式容纳它们：

**定义1a. ** 一个问题可以分解为问题所需的一系列概念（基本技能）。由于问题可能会要求学生重复一次或多次重复某些技能，因此我们使用一组表示为p(s)的基本技能来表征问题的难度

定义1b。我们说，如果且仅当p（s1）⊒ p（s2）时，问题s1至少与s2一样困难，表示为s1≥s2。这意味着，如果学生能够解决s1，那么他/她也必须能够解决s2 [6]

这里⊒表示多集之间的超集关系。如果是p（s1）⊒（s2），那么对于问题2次所需的任何概念c，也至少也需要1次。例如，AABC⊒ABC为true，而AABCC⊒ABBC为true，因为ABBC有两个“ B”，而AABCC只有一个

定义1c。严格偏序1> s2定义为s1≥s2^s2≱s1，这意味着s1（严格来说）比s2难。

定义1d。如果说且仅当s1> s2并且没有其他问题3使得s1> s3> s2，我们说问题1比s2更难

使用定义1d，我们为一系列问题构建了层次结构，如下所示：

定义2.我们将一组问题S = {s1，s2，···}（我们称为普遍问题集）组织为偏序图G = 〈S，E〉，其中

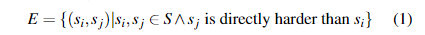
即，当且仅当sj比si直接困难时，才在部分排序图中存在从问题si到sj的（定向）边。图1显示了部分排序图的示例。

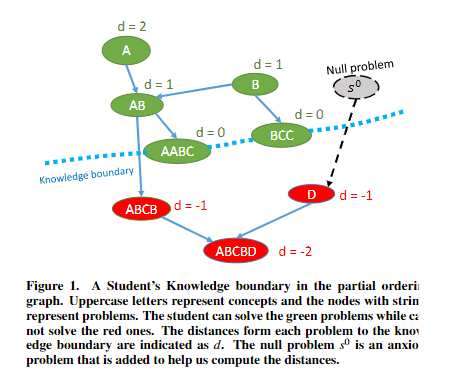
图一（部分排序图中的学生知识边界。大写字母表示概念，带有字符串的节点表示问题。学生可以解决绿色问题，而不能解决红色问题。从每个问题到知识边界的距离以d表示。空问题s0是一个焦虑问题，被添加来帮助我们计算距离）

定义3.我们用知识边界K衡量学生的能力，知识边界K是学生可以解决的最困难的问题。形式上，如果这是学生可以解决的问题集，则

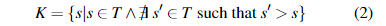
以图1中的偏序图为例。假设一个学生可以解决问题A，AB，B，AABC和BCC（图中的绿色节点），而不能解决ABCB，D或ABCBD（图中的红色节点）。然后，知识边界仅包含两个问题：AABC和BCC，因为没有其他“绿色”问题比AABC或BCC难。知识边界不包括A，AB或B，因为存在一个“绿色”问题AABC，比所有问题都难

计算知识边界

We present a graph coloring algorithm of calculating a stu-dent’s knowledge boundary in the partial ordering graph. Thisalgorithm is based on two properties of the partial ordering: ifa student can solve problems, he must be able to solve anyproblems′that is at most as hard as s(s≥s′); if a studentcannot solve problems, he must not be able to solve any prob-lems′that is at least as hard as s(s′≥s). For example, if astudent can solve problem AB, he/she can also solve problemsA and B; if a student cannot solve problem ABCB, then he/she cannot solve problem ABCBD either.

我们提出了一种图形着色算法，用于计算部分排序图中学生的知识边界。该算法基于偏序的两个属性：如果一个学生能够解决问题，那么他必须能够解决至多像s(s≥s’)一样困难的任何问题。如果学生不能解决问题，则他必须不能解决至少与 s(s’≥s) 一样困难的任何问题。例如，如果学生可以解决问题AB，那么他/她也可以解决问题A和B；如果学生不能解决问题ABCB，那么他/她也不能解决问题ABCBD。

At the start of the algorithm, all the problems (nodes) in thepartial ordering graph are uncolored. The algorithm asks thestudent whether he/she can solve some problem s*. If thestudent can solve s*, all the nodes that are at most as hard as s*(including s* itself) will be colored ‘solvable’; if the studentcannot solve s*, all the nodes that are at least as hard as s* (including s* it self) will be colored ‘unsolvable’. Figure 2 shows how this coloring process works.

在算法开始时，部分排序图中的所有问题（节点）都是未着色的。该算法询问学生是否可以解决某些问题s*。如果学生能够求解s*，则所有与s*一样难的节点（包括s*本身）将被着色为“可求解”；如果学生不能求解s*，则所有至少s*同等困难的节点（包括s*自身）将被着色为“无法解决”。图2显示了此着色过程的工作方式。

The algorithm repeatedly selects an uncolored problem s* from the partial ordering graph, asks the student to solve it, and then updates the coloring of the graph based on the response. Thisis a greedy algorithm designed to minimize the number ofproblems that must be given to the student. Formally, if $n^+_s$ denotes the number of the uncolored problems that are at mostas hard as $s$ , and $n^-_s$ denotes the number of the uncolored problems that are at least as hard as s, then we can maximize thenumber of problems that can be colored based on the student’s response by greedily selecting a problem s* as follows:

该算法从偏序图中反复选择一个无色问题s*，要求学生解决它，然后根据响应更新该图的颜色。这是一种贪心算法，旨在最大程度地减少必须给学生的问题。形式上，如果 $n^+_s$ 表示最多没有硬色问题的无色问题的数量，而 $n^-_s$ 表示至少至少像s一样硬的无色问题的数量，那么我们可以使可以通过贪婪地选择问题s*，根据学生的回答进行着色：

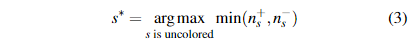
预测特定问题的表现

到知识边界的距离 Distance to Knowledge Boundary

In order to recommend problems at appropriate difficulty levels to the students, we need to predict students’ performanceon problems. Existing IRT studies have proposed several popular models stipulating how student performance is related tostudent ability [46, 53]. However, they measure a student’sability and the difficulty of a problem using unidimensionalnumeric scores, which is incomprehensive [28].

为了向学生推荐适当难度的问题，我们需要预测学生在问题上的表现。现有的IRT研究提出了几种流行的模型，这些模型规定了学生的表现与学生能力之间的关系[46，53]。但是，他们使用一维数字分数来衡量学生的能力和问题的难度，这是不全面的[28]。

Ideally, prediction of a student’s performance would utilizemultidimensional metrics to measure the distance between aproblem and what a student already knows. The key technicalchallenge in the design of multidimensional metrics is thatit is impossible to measure this distance without taking intoaccount the hierarchical structure of the problem space. In ourframework, we can measure this as the distance from the prob-lem to the knowledge boundary in the partial ordering graph.We use signed numbers to distinguish which ‘side’ of theknowledge boundary a problem is on: problems ‘inside’ theboundary (which the student can solve) have positive distanceswhile problems ‘outside’ the boundary (which the student can-not solve) have negative distances. Using this distance, wecan leverage IRT models to predict a student’s performanceon new problems.

理想情况下，对学生成绩的预测将利用多维指标来衡量问题和学生已经知道的知识之间的距离。多维度量设计中的关键技术挑战是，如果不考虑问题空间的层次结构，就无法测量该距离。在我们的框架中，我们可以用偏序图中图中从问题到知识边界的距离来衡量这个问题。学生可以解决）的距离为正，而“超出”边界的问题（学生无法解决的）的距离为负。利用此距离，我们可以利用IRT模型来预测学生在新问题上的表现。

Here, we give the definition of this distance together with theexamples in Figure 1. Assume we have the universal problem set S, and a student can solve a subset of problems T. For example, in Figure 1,S={A, AB, B, AABC, BCC, ABCB, D,ABCBD},T={A, AB, B, AABC, BCC}, and the knowledge boundary K={AABC, BCC}. We calculate the distance fromany problems∈Sto the knowledge boundaryK, indicated as d(s, K), following the steps below:

在这里，我们给出该距离的定义以及图1中的示例。假设我们有通用问题集S，并且学生可以解决问题T的子集。例如，在图1中，S = {A，AB， B，AABC，BCC，ABCB，D，ABCBD}，T ＝ {A，AB，B，AABC，BCC}，知识边界K ＝ {AABC，BCC}。我们按照以下步骤计算从任何问题∈S到知识边界K的距离，表示为d(s, K)：

Step 1: Calculate distances for problems on the boundary

步骤1：计算边界上问题的距离对于任何问题，

For any problemssuch thats∈K,d(s,K) =0.

对于任何问题s使得s∈K，d(s, K)= 0

For example, the distance of problems AABC and BCC is 0

例如，问题AABC和BCC的距离为0例如，问题AABC和BCC的距离为0

Step 2: Calculate distances for problems inside the boundary

步骤2：计算边界内问题的距离

For any problem s such that s∈T−K, based on the definition of K, there must be one or more s′∈K such that s′≥s (otherwise, s should be contained in K) , and

对于基于s的定义s∈T-K的任何问题s，必须存在一个或多个s′∈K使得s′≥s（否则s应该包含在K中），并且

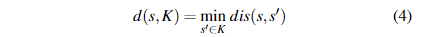
where d is(s,s′) indicates the length of the shortest directed path from s to s′ in the partial ordering graph. If there is no directed path from s to s′, dis(s,s′) =∞. Note that if s′≥s ,then there must exist at least one directed path from s′ to s.

其中d is（s，s’）表示部分排序图中从s到s’的最短定向路径的长度。如果没有从s到s’的定向路径，则dis（s，s’）=∞。请注意，如果s’≥s，则必须存在至少一条从s’到s的定向路径。

For example, the distance of problem AB is 1, since prob-lem AABC, which is on the knowlegde boundary, is directlyharder than AB. Similar for problem B (BCC is direclty harderthan B). The distance of problem A is 2, since the shortest di-rected path from A to any problem on the knowledge boundary(which is A→AB→AABC) has length 2

例如，问题AB的距离为1，因为在知识已知边界上的问题AABC比AB直接困难。与问题B相似（密件抄送比B硬）。问题A的距离为2，因为从A到知识边界上任何问题的最短定向路径（A→AB→AABC）的长度为2

Step 3:Calculate distances for problems outside the boundary

步骤3：计算边界外问题的距离

In a hierarchical knowledge structure, it follows intuitively thatproblems that are further away from the boundary will be moredifficult to the student. Therefore, for any problemssuch thats∈S−T, we define the distanced(s,K)to be shortest directedpath from any problem inTtos. Note that this distance alsohas a teaching interpretation: if easier problems should alwaysbe taught before harder problems [55], then this distance alsomeasures the number of problems that need to be taught beforeteachings.

在分层的知识结构中，直观地认为，远离边界的问题对学生而言将更加困难。因此，对于诸如s∈ST的任何问题，我们将距离（s，K）定义为距Ttos中任何问题最短的有向路径。注意，这个距离也有一个教学上的解释：如果总是在较困难的问题之前总是先教更容易的问题[55]，那么这个距离也可以衡量在教学之前需要教的问题数量。

ince there are some basic problems that have no problemseasier than them, and thus have no incoming edges in the par-tial ordering graph, there is not always a path from a probleminTtos. For instance, there is no directed path from anyproblem inTto problemDin Figure 1. To resolve this, weadd anull problems0, the pseudo problem with no prerequisiteconcepts, toT. For any problems∈S−T, if there is no otherproblems′such thatsis directly harder thans′(namely,shas no incoming edges), we add an edge(s0,s)to the partialordering graph

由于存在一些基本问题，没有比这些问题更容易解决的问题，因此在空间排序图中没有传入的边，因此从问题中获取问题的路径并不总是那么容易。例如，图1中没有从任何问题到问题D的直接路径。要解决此问题，我们将无问题先决条件的伪问题anull问题0添加到T。对于任何问题∈ST，如果没有其他问题’使假设比’s’直接困难（即没有进入的边），我们将偏边（s0，s）添加到偏序图

Now there is at least one directed path from the null problem s0 or some problem in T to s. We can define the distance as:

现在，从空问题s0或T tos中的某个问题开始，至少有一条有向路径。我们可以将距离定义为：

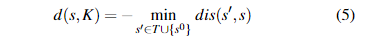
Note that d(s,K) is negative if and only if s is outside the knowledge boundary.For example, the distance of problem ABCB is -1, since itis directly harder than the “green” problem AB. Problem D has no incoming edges in the partial ordering graph, hence weadd an edge from the null problem s0 to D, and the distanceof problem D is -1 since the path s0→D has length 1. Lastly,the distance of problem ABCBD is -2. Actually, there aretwo shortest paths with length 2: AB→ABCB→ABCBD ands0→D→ABCBD.

请注意，当且仅当s在知识边界之外时，d(s, K)才为负。例如，问题ABCB的距离为-1，因为它比“绿色”问题AB直接困难。问题D在偏序图中没有输入边，因此我们将零问题s0到D加上一条边，并且由于路径s0→D的长度为1，因此问题D的距离为-1。最后，问题ABCBD的距离为 -2。实际上，有两条最短的路径，其长度为2：AB→ABCB→ABCBD和s0→D→ABCBD。

The metric of distance is dependent on the density of thepartial-ordering graph. This is inevitable since the measure-ment is based on the hierarchical structure of the problemspace. We believe that for most well-defined problem spaces,it is a reasonable assumption that the partial ordering graph will be sufficiently dense. We will demonstrate this metricworks well for a well-built Japanese language learning corpusin the next section

距离的度量取决于偏序图的密度。这是不可避免的，因为测量是基于问题空间的层次结构。我们认为，对于大多数定义明确的问题空间，可以合理地假设偏序图将足够密集。我们将在下一部分中很好地演示此度量标准，以构建完善的日语学习语料库。

In the later part of this paper, we will use d to denote d(s,K) for convenience

在本文的后半部分，为方便起见，我们将使用d来表示d(s, K)。

Adapted Rasch model 改编的Rasch模型

In this section, we describe how we can adapt existing uni-dimensional IRT models to build a multidimensional metricthat leverages the partial ordering graph and the distance d calculated in the previous section in order to predict studentperformance. One of the most famous models of IRT, the Rasch model [53], stipulates that a student’s performancePis a function of the difference between the student’s ability θ and the problem’s difficulty b

在本节中，我们描述如何适应现有的一维IRT模型以建立多维度量标准，该度量标准利用上一节中计算的偏序图和距离d来预测学生的表现。 Rasch模型[53]是IRT最著名的模型之一，它规定学生的表现是学生的能力θ与问题难度b之差的函数。

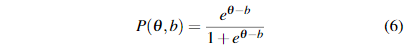
xxx

In the next section, we will demonstrate that this adaptedmodel nicely fits the data collected from our knowledge as-sessment platform

在下一节中，我们将证明该适应模型非常适合从我们的知识评估平台收集的数据

知识评估的评价 EVALUATION OF KNOWLEDGE ASSESSMENT

In this section, we will the evaluate our calculation of the knowledge boundary and the distance represented in the previous section by applying it to a Japanese language learning domain.

在本节中，我们将评估我们的知识边界与上一节中表示的距离的计算并把它应用到一个日语学习领域。

语言评估平台 J100: A Language Assessment Platform

xxx

Reddit部署 Reddit Deployment

xxx

验证知识边界和距离度量 Validating the Knowledge Boundary and Distance Metric

In order to validate our calculation of the knowledge boundaryand the distance metric, we will demonstrate that the user datacollected from J100 nicely fits the adapted Rasch Model. Wecalculate a user’s knowledge boundaryKbased on his/her responses to the problems in the assessment stage, and foreach problemsresponded in the evaluation stage, we measurethe distance from the problems to the knowledge boundary K.The user responses in the evaluation stage can be regarded as users’ self-estimation of their performance, and we score thefive possible responses uniformly from 1 to 0

为了验证我们对知识边界和距离度量的计算，我们将证明从J100收集的用户数据非常适合改编的Rasch模型。我们根据用户在评估阶段对问题的回答来计算用户的知识边界K，并针对评估阶段所回答的每个问题，测量从问题到知识边界K的距离。评估阶段中的用户响应可视为用户对他们的表现的自我评估，我们从1到0对5个可能的回答进行了统一评分

过程分析 PROGRESSION ANALYSIS

良好的进步会增强学生对课程的参与度[43,56]，我们的工作旨在发现良好的进步的一般特征。在本节中，我们将利用我们的框架来分析教育进度，并介绍良好进度的两个重要特征：组成Composition和步调Pace。我们研究了现有课程，并证明了专家设计的课程中一些惊人的相似之处

组成：学习与复习的平衡 Composition: The Balance of Learning and Review

在设计教育进度时，一个关键的考虑因素是应该花多少时间来增强以前引入的知识，而不是引入新知识。另一个需要考虑的问题是，通过以新的方式将概念组合在一起，进度是否应该越来越复杂。理想情况下，我们将能够定义可以简洁地捕获这些重要方面的进度参数空间

xxx

我们可以认为强化是对已学知识的回顾，引入是纯学习，重组是两者的混合。这三种类型的比例揭示了设计师在教育进步中平衡学习和复习的策略，我们将其称为进步组成

步调：知识的增长率 Pace: The Growth Rate of Knowledge

我们想知道进度中课程（章节，单元等）的难度是否以一致的速度增长，从而使学生可以顺利学习。我们不是通过数字来衡量每节课的难度，而是计算知识的大小，即每节课之前引入的问题总数。这可以用通用问题集5S中的问题数量来衡量，该数量被学生的知识边界归类为强化。在掌握了从一开始到当前课程的所有知识之后。因此，知识大小| K |就是此类问题的数量

进度分析的评估

教材研究

在线语言学习工具研究

自动渐进合成

We have discussed two features of an educational progression:composition and pace. In this section, we will demonstratethat educational progressions can be automatically synthesizedaccording to specific composition and pace parameters. To bemore precise, a progression can be characterized as three nu-meric parameters: overall pace (pace), proportion of reinforce-ment (ri), and proportion of introduction (in). The proportionof recombination (rc) is redundant since ri+rc+in=1.

我们讨论了教育进步的两个特征：组成和步调。在本节中，我们将证明可以根据特定的构成和速度参数自动合成教育进度。更准确地说，可以将进度表示为三个数字参数：总体步速（步幅），增强比例（ri）和引入比例（输入）。重组比例（rc）是多余的，因为ri + rc + in = 1

We use a greedy algorithm to synthesize progressions. Thealgorithm starts with an empty progression, repeatedly selectsthe next problem that minimizes the following error function and appends it to the progression:

我们使用贪婪算法来合成进度。算法以空的级数开始，重复选择下一个使后继误差函数最小化的问题，并将其附加到级数上

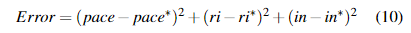
其中pace, ri, in 都是实际的渐进特性，而pace*, ri*, in*是所需的渐进参数。请注意，可能存在多个具有最小误差的问题。在这种情况下，我们的算法会从中随机选择一个作为下一个问题

这种贪婪算法并不总是生成具有准确所需参数的级数。但是，它运行得非常快。对于一个包含25个问题的通用问题集，它可以在一秒钟内合成100多个进程（每个进程有10个问题），因此，我们可以多次运行此贪婪算法以合成具有所需特征的进程

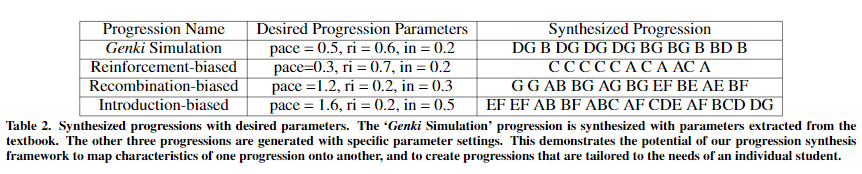
表2列出了合成过程的四个例子。我们从Genki进程中提取了以下参数：pace= 0.465，ri = 0.582，in = 0.214。然后，我们使用这些参数（大约）来合成“ Genki Simulation”进度。我们还生成了另外三个带有量身定制的参数的进度，这些进度偏向于加强，重组和引入。这些结果表明，我们不仅可以利用专家级进度设计的原理并使用对大多数学生都有利的参数来综合进度，而且还可以为具有特定偏好的学生量身定制进度

结论与未来工作

可学习性对于HCI的许多方面都很重要：用户界面，学习工具，视频游戏和软件可用性。在本文中，我们定义了一个框架，该框架利用自动问题分解和部分排序图构造来促进与教育相关的多个工作流程：评估学生的知识，确定和描述课程的学习策略以及设计新的学习进度。我们以多种方式评估了该框架：通过在线部署日语评估工具，自动从现有课程中提取起搏参数，以及将问题组合成符合所需起搏特征的新项目

我们希望将我们的框架用于几个教育领域，尤其是计算机辅助语言教育。例如，我们计划利用我们的框架向第二语言学习者推荐适当的阅读材料，并改善用于语言学习的教育游戏[17，18]。将来，我们不仅将框架应用于语法知识，还将应用于语言学习的其他方面，例如词汇和语义

我们希望这些想法将有助于实现一门进行性分析的科学，在该科学中，可以从涉及多个主题的进展中提取出测序和起搏参数，以识别最佳原则。此外，我们希望扩展此框架，以便它可以自动构建能够快速进行初始评估和进度调整的自适应学习系统