fit5163-sec-notes
这门课是Blockchain的前置课。
主要讲的是一些安全方面的内容。
assignment两个,一个是期中考试(15%),一个叫mini research应该是论文解读相关(25%)。
剩下60%是考试。
平时tut主要是带你做题目方式答疑,tut和lec之间每周内容对应(这周lec这周tut讲完
W1: Intro
定义了一下各类术语,以及进行一些分类。
考点:标准,攻击,服务,机制
Security standards 安全标准
网络安全标准Cybersecurity standards:
are techniques set forth in published materials that attempt to protect the cyber environment of a user or organization, 例如AES(from NIST)
- 国际标准International standards: ISO/IEC 27000(澳洲用), ITU-T X.800, IEC 62443
- 国家标准: US: NIST, FIPS140; UK: Cyber Essentials
术语(会让你说这个事/物算哪个,经常问Threat和Vulnerability和Risk)
-
Adversary (threat agent, attacker, hacker): Adversary意思是对手
-
Threat: 违反安全的可能性(potential),当存在可能违反安全并造成伤害的情况、能力、行动或事件时,就存在这种可能性。
-
Vulnerability: 系统设计、实施或操作和管理中的缺陷或弱点,可被利用来违反系统的安全策略。
-
Attack: 源自智能威胁的对系统安全的攻击; 故意逃避安全服务并违反系统的安全策略
-
Countermeasure对策: 通过消除或防止威胁、漏洞或攻击,通过最大限度地减少其可能造成的伤害,或通过发现和报告它以便采取纠正措施来减少威胁、漏洞或攻击的行动、设备、程序或技术
-
Risk: 损失预期,表示为特定威胁利用特定漏洞并产生特定有害结果的可能性。
-
Security Policy: 一组规则和实践,指定系统或组织如何提供安全服务以保护敏感和关键系统资源。
-
System Resource (Asset) - Data: 系统提供的服务; 系统能力; 一项系统设备; 容纳系统操作和设备的设施。
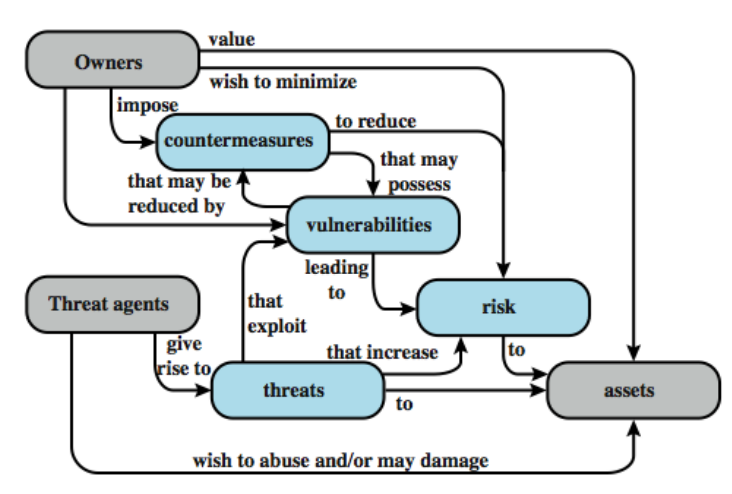
信息安全是关于如何防止攻击,或者如何防止攻击,以检测对基于信息的系统的攻击
信息安全的 3 个方面:
- 安全攻击/威胁:可能违反安全策略的一种可能方式(例如,完整性或机密性的丢失)。
- 安全服务:一种可以用来应对威胁或反击攻击的措施(例如提供保密性)。
- 安全机制:提供服务的手段(例如加密、数字签名)
Security attacks 安全攻击
General Well-Known Threats 常见威胁
• Viruses, worms, trojans
• Malware • Phishing
• Botnets
• Brute-force
• DoS/DDoS
• Man-in-the-middle
• SQL injection
Resources/Assets
- Information/data: Password, credit card, e-health records
- Service: Storage service, data process services
- Hardware: RAM, cache, hard disks, branch predictor units, GPU
- Software
- Firmware: BIOS
动机
- Obtain/access private resources → Confidentiality
- Bypass authentication for accessing private resources→ Authentication
- Break the availability of a service → Availability
- Breach the integrity of information → Integrity
分类
Passive attacks
- Interception: an attack on confidentiality 只嗅探这样
Active attacks
- Interruption: an attack on availability: DoS这样影响了可用性
- Modification: an attack on integrity
- Fabrication: an attack on authenticity & integrity
- Replay: an attack on freshness
Security services 安全服务
旨在对抗安全攻击
利用一种或多种安全机制来提供服务
6 项主要安全服务/财产/目标:
• Confidentiality
• Integrity
• Availability
• Authentication
• Non-repudiation 不可否认性:防止通信中的一方否认
• Access control
信息安全的主要重点是平衡保护数据的机密性、完整性和可用性(也称为 CIA triad三元组)
技术手段
- Confidentiality-> encryption
- Integrity -> Message Authentication Code (MAC); Message Authentication Code (MAC); Digital signature
- Availability-> High availability systems
- Authentication -> What U know: PIN, or a password; What U have: a driver’s license or a magnetic swipe card; What U are biometrics, including palm prints, fingerprints, voice prints and retina (eye) scans
- Non-Repudiation: Digital signature; Message Authentication Code (MAC)
- Access Control: File permissions in Unix/NT file systems
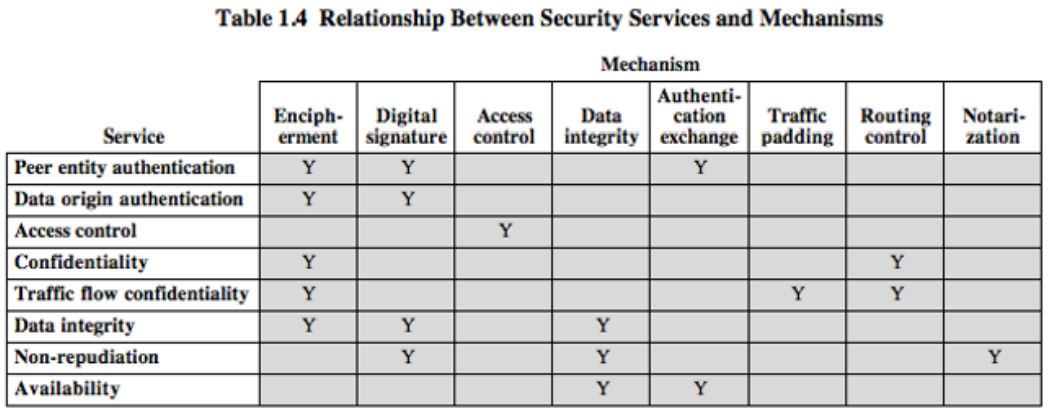
Security mechanism 安全机制
Specific security mechanisms: 用于提供特定的安全服务
Pervasive security mechanisms: (遍布的,普适的)不特定于特定服务
Specific Security Mechanisms
• Encipherment (encryption) : hide or covers data
• Data integrity
• Digital signatures
• Access controls
• Authentication exchange: 通过信息交换确保实体的身份
• Traffic padding: 将bits插入数据流中的间隙以阻断流量分析尝试
• Routing control: 选择并不断改变发送方和接收方之间不同的可用路线
• Notarization 公证; 使用受信任的第三方来控制双方之间的通信
Pervasive Security Mechanisms
• Trusted functionality: 可用于扩展范围或建立其他安全机制的有效性; 任何直接提供或提供对安全机制的访问的功能都应该是值得信赖的
• Security labels: 系统资源可能具有与其相关联的安全标签,例如,用于指示敏感度级别(绝密、机密、机密、未分类); 通常需要在传输数据时传送适当的安全标签
• Event detection: 检测与安全相关的事件
• Security audit trails 安全审计追踪: 过去与安全相关的事件的日志; 允许检测和调查过去的安全漏洞
• Security recovery: 包括处理从安全故障中恢复的请求的机制; 可能包括操作的立即中止、实体的临时失效、将实体添加到黑名单
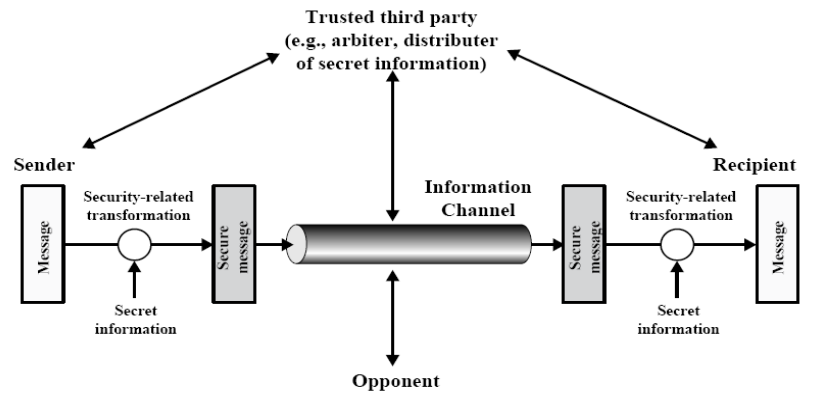
Model of system/(inter)network security 系统/网络安全模型
主要会问到底属于 系统/网络间/网络内 的安全问题
Network Security
Tut: 数学回顾
质数分解,GCD 略
Congruent class of each number每个数字的全等类->就是算余数
Eulers Totient φ(n) : φ(n) = (p − 1) × (q − 1) if p and q are primes.
a truth table: ¯表示取反
| x | y | x + y | x + ¯y | ¯x + y | (x + y)(x + ¯y)(¯x + y) | xy |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
⊕表示XOR抑或(= (x!=y) )
| x | y | ⊕ |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
W2: 加密规则 Principles of Encryption
加(解)密的一些原理
考点:传统密文(Substitution,Transposition,Product 以及language statistics的安全分析),加密系统特性(Avalanche effect 雪崩效应,Unconditional security,Computational security),加密分析(各种攻击)
术语
• Plaintext – 原始消息
• Ciphertext – 编码/加密的消息
• Cipher –明文和密文之间的转换算法
• Key – 密码中使用的秘密信息,只有发送方和接收方知道
• Encrypt/encipher – 明文转换为密文
• Decrypt/decipher – 密文转换为纯文本
• Cryptography – 安全通信技术的研究
• Cryptanalysis (codebreaking) – 分析密码技术的研究(不知道密钥)
• Cryptology – 密码学和密码分析领域
Caesar Cipher: 熟悉的置换(Substitution)比如ABCD -> EFGH,即
C = Enc(k, P) = (P + k) mod 26
P = Dec(k, C) = (C – k) mod 26
如果 (a mod n) = (b mod n) ,则 a 和 b 被称为模 n 全等; 等价于 a Ξ b (mod n)
r 称为a mod n 的残差, a = qn + r。 通常选择最小的正余数作为残差(-12 mod 7 = 2 mod 7 = 2)
Monoalphabetic Ciphers 单字母密码
单字母密码: 每个明文字母映射到不同的随机密文字母
攻击: 单字母替换密码不会改变相对字母频率
计算密文的字母频率-> 将计数/图与已知值进行比较
常见的双/三字母表也有帮助->碰瓷the这类单词
Polyalphabetic Ciphers 多字母密码
多字母密码: 在处理明文消息时使用不同的单字母替换
Vigenère Cipher维吉尼亚密码: 用一个和Ptxt等长的Key,密文Ctxt[i] = Ptxt[i] + Key[i] mod 26
• 每个明文字母有多个密文字母, 字母频率被掩盖。但是,并没有完全迷失
• 破解密码取决于猜测密钥长度: 例如 “红色”的 2 个实例由 9 个字符位置分隔。
• 使用语言频率分别攻击每个单字母密码
具体攻击实现 Kasiski Method
密文中的重复提供有关关键字长度的线索
->查找重复文本块之间的距离
->这些块的公约数给出了关键字长度(概率很高)例如重复的“VTW”——建议密钥大小为 3 或 9
->然后,使用与以前相同的技术单独攻击每个单字母密码
One-Time Pad: 使用真正随机,与Ptxt等长,的Key
• 始终存在将明文映射到密文的密钥
• 今天的计算机化应用:明文位与真正随机的密钥位进行异或
缺陷:
• 需要生成很长的密钥 – 同时分发和存储这些长密钥
• 密钥需要真正随机
• 此外,同一个密钥只能使用一次
Transposition Ciphers换位密码
略
Rail Fence cipher栅栏密码
略
Product Ciphers乘积密码
略
Desirable Properties 理想的属性
- No information loss:
- Ciphertext needs to completely obscure statistical properties with respect to the original message: 密文需要完全掩盖原始消息的统计属性
- Confusion: 使密文和密钥之间的统计关系尽可能复杂 > 通过substitution替换实现
- Diffusion: 每一位密文都应该受到每一位明文和密钥的影响(复杂的关系应该在所有位之间传播) > 通过transposition/permutation转置/排列实现
- Avalanche effect 雪崩效应:
明文或密钥的微小变化会导致密文发生重大变化
一位明文或密钥的变化应该会导致密文的许多位发生变化
->使猜测密钥的尝试变得不可能 - From the view of information security we would like to have unconditional security从信息安全的角度,我们希望有无条件的安全: 无论有多少计算机能力可用,密码都无法破解,因为密文提供的信息不足以唯一确定相应的明文
- From the view of computational efficiency we would like to have computational security从计算效率的角度来看,我们希望有计算安全性: 计算成本/时间>>攻击成本/时间
General Attacks
- Cryptanalytic attack 密码分析攻击
- Brute-force attack 略
Cryptanalytic attack 密码分析攻击
攻击依赖于算法的性质加上对明文一般特征的一些了解
攻击利用算法的特性来尝试推断特定的明文或推断使用的密钥
- Ciphertext only attack: 攻击者只能访问密文; 不知道什么明文加密为给定的密文; 最弱的攻击者
- Known plaintext attack: 攻击者可以访问 ( ptxt , ctxt ) 对,其中 ctxt =Enc(ptxt); 但是,不能选择出 (ptxt , ctxt) 对; 目标是破解明文未知的密文或恢复出密钥
- Chosen plaintext attack: 攻击者可以访问 ( ptxt , ctxt ) 对,其中 ptxt 由攻击者选择; 与已知明文攻击的目标相同
- Chosen ciphertext attack: 攻击者可以访问 ( ptxt , ctxt ) 对,其中 ctxt 由攻击者选择; 与已知明文攻击的目标相同
- Chosen text attack: 攻击者可以访问 ( ptxt , ctxt ) 对,他可以在其中选择 ptxt 或 ctxt; 最强攻击者
在所有这些中,始终假设加密/解密算法是已知的,但密钥不知道!
Brute-Force Attack
涉及尝试每个可能的密钥,直到获得密文到明文的可理解的翻译
平均而言,必须尝试所有可能的密钥的一半才能成功
为了补充蛮力方法,需要对预期的明文有一定程度的了解,还需要一些自动区分明文和“垃圾”的方法
Tut: Intro
一堆文字题……
W3: 对称加密 Symmetric Cryptography
大家熟悉的AES案例
更侧重讲的是Block的,stream的部分是放在了W2结尾
考点:流密码(RC4),块密码DES/AES,块密码的模式,MAC
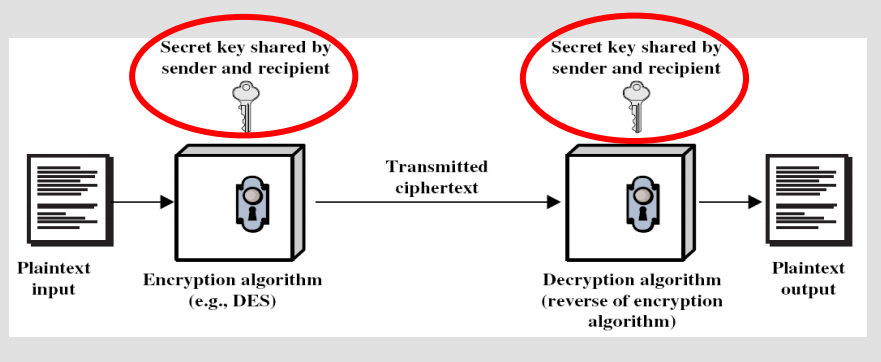
规则
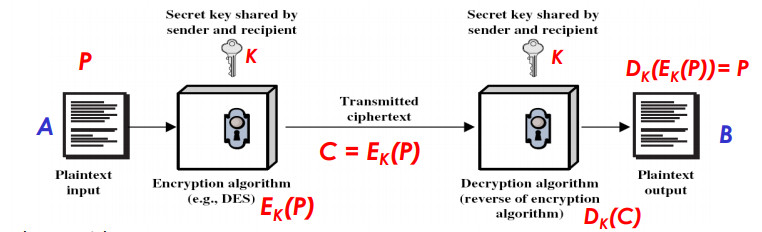
- 与 共享一个密钥 ,密钥可由密钥分发中心 (KDC, key distribution center) 分发。
- 通过应用加密函数 和密钥 来加密明文消息 以创建密文
- 通过通信信道将密文 发送给 。 即使 B 以外的其他人获得了 的副本,除非他拥有 ,否则他无法解密该消息。
- 如果密钥分发是完美的,或者 没有意外或故意泄露密钥,那么除了 之外没有人应该拥有密钥 。
- 在接收到 时, 使用密钥 在 上应用解密函数 以恢复明文消息 P:
对称密码
Stream cipher: ➢ 连续处理输入元素 ➢ 一次产生一个元素(1 位或 1 字节) ➢ 例如,RC4 和rabbit
Block cipher:➢ 一次处理一个输入块 ➢ 为每个输入块产生一个输出块 ➢ 例如,3DES 和 AES
Stream Cipher
流密码属性
• 一些设计注意事项是:
– 没有重复的密钥流的长周期
– 密钥流在统计上是随机的
– 种子(主密钥)足够长且随机(128-256 位)
– KSG 函数很难反转
• 如果设计得当,可以像具有相同大小密钥的块密码一样安全
• 但通常更简单、更快
• 示例:RC4
RC4
• 目标:为明文的每个字节生成一个字节(8 位)
• 主要思想:以“随机”方式从 256 个候选者中挑选一个值
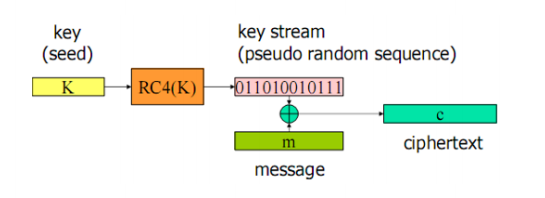
• RC4 逐字节加密明文
• RC4 提供了一种以“随机”方式从 256(即 )个候选中挑选一个值的方法
- Initialize an array of 256 bytes T (initial state of S & T) S=Seed T[i]=K[i mod keylen]
- KSA(Key Schedule Algorithm, permutation of S), S内部Swap
- Key Stream Generation, Ci = Mi XOR S[t]
由于 RC4 是一种流密码,绝不能重复使用相同的密钥流!– 相同的密钥在 RC4 中提供相同的密钥流!
这个想法是通过诉诸计算安全性使“一次性密码”变得实用
• 步骤:
1)从一个小密钥(“种子”)生成一个长密钥流
2) 将密钥流与消息进行异或
• 密钥流称为“伪随机”
– 不像一次性纸垫那样真正随机!
– 与消息长度相同
• 密钥流的随机性破坏了消息中的统计属性
𝑀: 消息
𝜅: 主键
𝐾: 生成的密钥流
𝐼𝑉: 初始化向量,所有人可知非私密
• 2 个步骤(形式化):
- 𝐾 ← 𝐾𝑆𝐺(𝜅,𝐼𝑉),其中 KSG 是一个“密钥流生成器”
- 𝐶 = 𝑀 ⊕ 𝐾
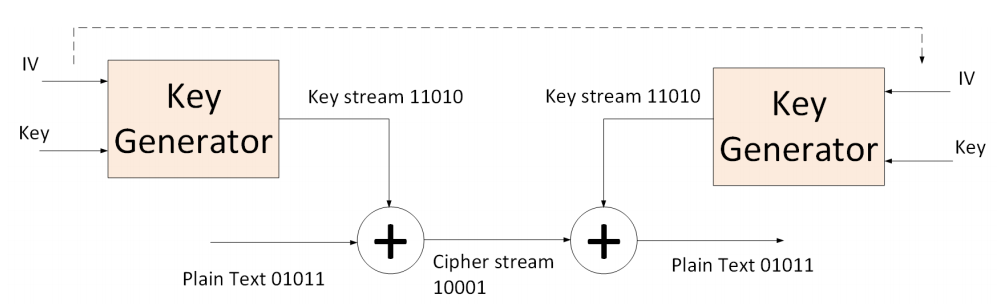
密钥流生成器 (KSG) 或伪随机生成器 (PRG) 是一种确定的过程,它将随机种子 (Key) 映射到无法(在计算上)与随机字符串区分开的较长伪随机字符串。
Seed/Main Key通常是从均匀分布中随机抽取的短二进制字符串
Block Cipher
Feistel Cipher: 许多分组密码算法,包括 DES(数据加密标准),都具有由 IBM 的 Horst Feistel 于 1973 年首次描述的结构。“Feistel Cipher/Network/Structure”本身并没有描述具体的分组密码,而是设计分组密码的一般方法
• 将明文分成两等份 (𝐿0, 𝑅0)
• 第𝑛 轮次处理二分之一
• 对于每一轮 𝑖 = 1,2, … , 𝑛
𝐿𝑖 = 𝑅𝑖−1
𝑅𝑖 = 𝐿𝑖−1 ⊕ 𝐹(𝑅𝑖−1,𝐾𝑖)
其中 𝐹 是轮函数,𝐾𝑖 是子密钥或轮密钥
• 在第 𝑛 轮之后,密文是 (𝐿𝑛, 𝑅𝑛)。
• 不管函数𝐹,解密是通过
𝑅𝑖−1 = 𝐿𝑖
𝐿𝑖−1 = 𝑅𝑖 ⊕ 𝐹(𝐿𝑖 ,𝐾𝑖)
• 16 轮的示例图


左:加密; 右:解密
Block size块大小:更大的块大小意味着更高的安全性
Key size密钥大小:较大的密钥大小意味着更高的安全性
Number of rounds 轮数:更多轮提供更高的安全性,通常为 16 回合
Subkey generation algorithm子密钥生成算法:复杂度越大,密码分析难度越大
Round function 每轮函数:更大的复杂性意味着更大的阻力
(但是要考虑到convenience
DES
Feistel structure; Cipher: Block;
Block size: 64 bits; (Effective) Key size: 56 bits (=64-8)
16 subkeys created for 16 rounds
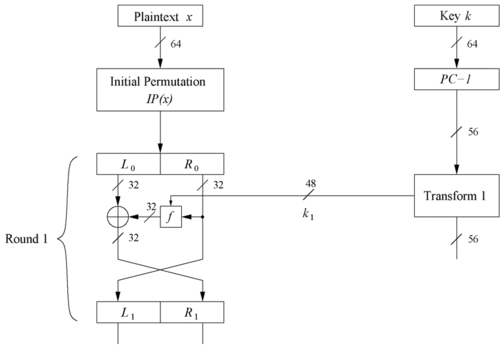
IP初始化置换: 把x整成一个ixj的矩阵(将原块中的第 n 位放入新块的 (8* i+j 位
Round Function:
- 明文被分成 32 位的一半 和
- 被送入函数 f ,然后对其输出进行异或运算
与 - 左右半边互换
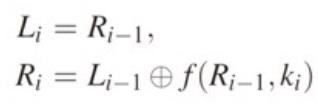
函数 f 输入和每轮的key :
-
扩展E(增加漫射diffusion): 把一个32bits扩展到48(6x8)bits。n 位于第 i 行第 j 列表示,将原块中的第 n 位放入新块的第 (6* i+j) 位
-
与轮key计算异或: 轮密钥和扩展 E 的输出的按位异或; 轮密钥派生自 DES 密钥表中的主密钥(在少数
-
S-box矩阵替换(DES 安全的关键要素!非线性且抗差分密码分析): 8个表,6bits输入,4bits输出
-
置换(增加漫射diffusion): 按位排列; 一个 S Box 的输出位会影响下一轮的多个 S Box。
E、S 盒和 P 的Diffusion 确保了在第 5 轮之后每一位都是每个密钥位和每个明文位的函数
最后一轮后,进行反向IP操作
DES的Subkey生成
DES 需要 16 个来自原始 56 位密钥的 48 位轮密钥/子密钥
输入key大小为 64 位:56 位key和 8 位parity(校验)
步骤:
- 丢弃 8 个校验位
- 置换bits
- 分成两个28位
- 往左旋转1bit(在第 1、2、9 和 16 轮的进行1bit;剩余轮次(3,4,5,6,7,8,10, …15)移动2bits )
- 置换并提取 48 位作为子密钥
主要问题:密钥长度太小!
S Boxes的设计一直保密
还有密码分析攻击;差分密码分析,线性密码分析,…
它们在实践中不会构成真正的威胁,但对于了解安全方面仍然很重要
如何在不需要大改动的情况下解决这些问题?3DES
3DES
应用DES算法3次;使用 3 个密钥和 3 次执行 DES 算法(加密解密加密):略
其他加密算法
International Data Encryption Algorithm (IDEA); Blowfish; RC5
AES
1997年,美国国家标准与技术研究院(NIST)正式启动高级加密标准(AES)比赛,以取代DES。基于:安全性、计算效率、内存要求、软硬件适用性、灵活性
由比利时的 Joan Daemen 和 Vincent Rijmen 开发,也称为 Rijndael 算法
AES 是一种Block cipher
设计简单/灵活/高效,适用于软件和硬件的实现,以及许多 CPU 上的代码紧凑性。
由于更大的块大小和更长的密钥,AES 提供了更高的安全性。
提供了很大的灵活性:AES 通常足够灵活,可以处理 32 位的任意倍数的密钥和块大小,最小为 128 位,最大为 256 位。
安全性:抵抗功耗分析和其他实施攻击
足以满足当今的大多数需求
规格:
固定块长度:128 位
3 种不同的密钥长度:128、192 和 256 位
密码由 N 轮组成,其中轮数取决于密钥长度:16 字节(128 位)密钥 10 轮;24 字节(192 位)密钥 12 轮;32 字节(256 位)密钥的 14 轮。
每个变换都采用一个或多个 4 x 4 矩阵作为输入,并生成一个 4 x 4 矩阵作为输出。 被称为state状态
密钥扩展函数生成 N + 1 个轮密钥,每个轮密钥是一个不同的 4 x 4 矩阵
结构:
前 N-1 轮由 4 个组成部分组成:
-
字节替换 Byte substitution(每个字节使用 1 个 S box)
- 每个字节被由 16x16 表的行(左 4 位)和列(右 4 位)索引的字节替换
-
移动行(简单置换 simple permutation):第 1 行:不移位,第 2 行:1Byte 左循环移位,第 3 行:2Byte 移位,第 4 行:3Byte 移位
- 在 ShiftRows 步骤中,状态的每一行中的字节循环向左移动。 对于每一行,每个字节移位的位置数逐渐不同。
-
混合列(混合state bits)
- 每列都使用固定矩阵进行转换(矩阵左乘以列给出状态中列的新值)
-
添加轮密钥(XOR state矩阵与扩展的key矩阵,每个ij求xor)
最后一轮 N 包含: SubBytes 、 ShiftRows 、(无混合列) 和 AddRoundKey
AES 128 needs 11 round keys
AES 192 needs 13 round keys
AES 256 needs 15 round keys
操作模式
块密码加密固定大小的块,例如 DES 使用 56 位密钥加密 64 位块
明文可以是任意长度,可以由多个块组成
在实践中需要某种方式来加密/解密任意数量的数据
NIST SP 800 38A 定义了 5 种操作模式
涵盖广泛的应用,可以与任何分组密码一起使用
5 种常用模式,其中明文、密钥和/或密文组合以加密/解密任意大小的块。每个都有不同的优点/缺点
- 电子码本 (ECB) 模式
- 密码块链接 (CBC) 模式
- 密码反馈 (CFB) 模式
- 输出反馈 (OFB) 模式
- 计数器 (CTR) 模式
ECB (Electronic Codebook) 模式
最简单的模式,每个块独立加密和解密
一次处理每个块(64/128 位)
输入数据被填充为块大小的整数倍
丢失的数据块不影响其他块的解密
错误不传播,仅限于单个块
所有块都使用相同的密钥加密
缺点:
- 相同的明文产生相同的密文
- 不隐藏模式
- 如果消息包含重复元素,则可以识别这些元素
- 流量分析是可能的
CBC (Cipher Block Chaining) 模式
最常用的模式,每个明文块与前一个密文块进行异或并加密
第一个明文块与初始化向量 (IV) 异或
每个块使用相同的加密密钥
在每个加密步骤之前加扰明文
更安全:相同密钥的不同消息对应不同的IV; 有效地重复模式不会暴露
缺点:
- 数据块的加密变得依赖于它之前的所有块
- 丢失的数据块将阻止对下一个数据块的解码
- 块不能并行加密(可以并行解密
- 明文的变化在密文中传播
CFB (Cipher feedback) 模式
在第一个块中,初始化向量 (IV) 被加密,然后与明文块进行异或
前一个密文块被加密,然后与每个明文块异或
每个块使用相同的加密密钥
CFB和CBC一样的优缺点
与 CBC 的区别:明文在每个加密步骤后会参与混淆
OFB (Output feedback) 模式
与CFB的区别:
- cipher 加密的输出用作下一个块的 IV,而不是最终块的密文
- 由于明文或密文仅用于最终的异或,因此可以预先执行分组密码操作,一旦有明文或密文可用,就允许并行执行最后一步。
CTR (Counter) 模式
一种“新”模式,虽然很早就提出了
与 OFB 类似,但使用计数器值而不是任何反馈值进行加密
每个明文块必须具有不同的计数器/随机数值(从未重用)
-
𝑂𝑖=𝐸𝐾(𝑖)
-
𝐶𝑖=𝑃𝑖⊕𝑂𝑖
用途:高速网络加密
优势:高效率
- 可以在硬件或软件中进行并行加密
- 可以在需要之前进行预处理
- 适用于突发高速链接
- 随机访问加密数据块
- 可证明的安全性(与其他模式一样好)
缺点
- 但必须确保不重复使用计数器值,否则可能会被破坏(参见 OFB)
Hash
哈希函数 H 是一种单向函数,它接受消息 M 并产生固定大小(例如 256 位)的输出(称为消息摘要或哈希值或指纹)
对于任何消息 M,很容易计算 h=H(M)
- One way property单向性质:给定 h,找到 x 使得 H(x)=h 在计算上是不可行的
- Collision resistance抗碰撞性:找到任何一对 (x, y) 使得 H(y)=H(x) 在计算上也不可行
- Deterministic确定性:相同的消息总是导致相同的散列
hash函数只将消息(不需要密钥)作为输入来生成消息摘要,任何人都可以计算任何值的哈希值!
如果输入仅相差 1 位,则输出将完全不同!
可以看作是一个确定性的伪随机函数(生成一个随机数)
包括 MD5、SHA 1、SHA 256 等。
Message Authentication Code (MAC)
(不是网卡那个哦,那个叫**media access control **address
MAC可以提供的服务:
- 完整性:确认消息未被更改
- 真实性:确认消息来自指定的发件人
MAC也作为标签
基于对称加密原型,由 3 部分组成:
- 生成密钥 K,在发送方和接收方之间共享
- 给定 K 和 m,生成: 𝑀𝐴𝐶=𝐶𝐾(𝑚)
- 给定 K、m 和 MAC,验证:𝑀𝐴𝐶=𝐶𝐾(𝑚)
MAC属性
将可变长度消息 M 压缩为固定大小的验证器:
MAC:{0,1}∗→{0,1}𝑛
是多对一(Many to one)功能:可能许多消息具有相同的 MAC; 但是在计算上很难找到具有相同 MAC 的 2 条消息
MAC 应该平等地依赖于消息的所有位
Message Code 功能
- HMAC(其实就是hash加盐,把盐拿来当key)
- 对称密码
- 基于密码的消息认证代码 (CMAC
- 认证加密

为AES加密提供认证(保证integrity
带有关联数据的身份验证加密 (AEAD) 操作模式
使用 Encrypt then MAC 方法
可以在其内部组件中使用具有 128 位块大小(例如 AES)的块密码
使用计数器模式的变体
提供机密数据的真实性(对称概念)(每次调用最多 64 GB)
在 NIST SP 800 38d 中标准化 GCM 加密:
-
加密机密数据
-
在机密数据和
-
任何额外的非机密数据
安全考虑:IV 不能被重用(在相同的密钥下)否则消息的保密性可能会受到损害
AES Counter Mode with CBC MAC (CCM)
具有关联数据的经过身份验证的加密
使用 MAC 然后加密方法
加密计数器模式
用于身份验证的 CBC MAC
在 RFC 3610 中提出,在 NIST SP 800 38c 中标准化
Nonce (IV) 不得重复(在同一密钥下),否则会危及安全性
Tut:
两个人通过对称密码进行通信需要多少密钥?
n个人安全通信需要多少把密钥?
答:1个秘钥。 n(n-1)/2 个密钥
A、B、C 是 n bit string
0 是一个 n 位的0
1 是一个 n 位的1
证明以下:
a. (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)
b. A ⊕ A = 0
c. A ⊕ 0 = A
d. A ⊕ 1 = bitwise complement of A = A’
e. (A ⊕ B)’ = A’ ⊕ B = A ⊕ B’
f. A’ ⊕ B’ = A ⊕ B
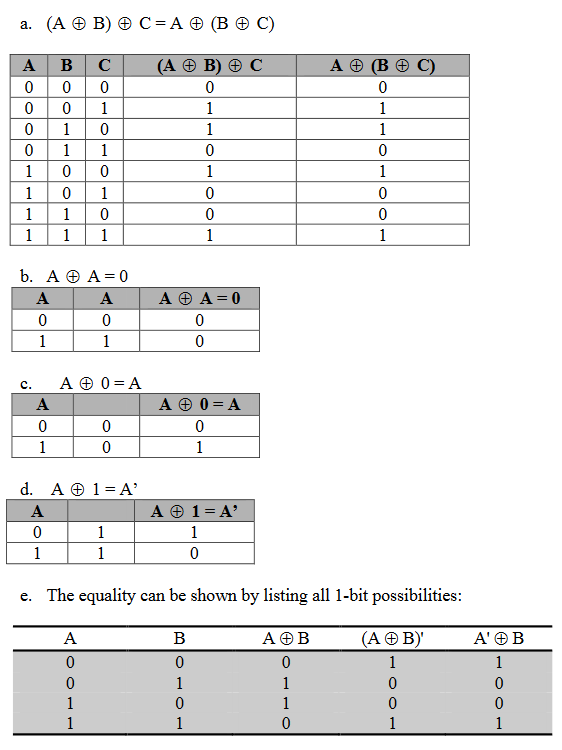
f. 我们还需要等式 A ⊕ B = A’ ⊕ B’,这很容易看出为真。(意思就是和e差不多
如果满足以下条件,密文的值是多少:
明文:1010101010100
密钥流:1100110001001
Ans :Ciphertext = Plaintext XOR keystream = 0110011011101 (XOR操作是根据图的定义得到的
在ECB模式下,如果传输的密文块中有错误,则只影响对应的明文块。 但是,在 CBC 模式下,此错误会传播。 例如,传输的 C1 中的错误(下面的图 6.4)显然会损坏 P1。
a. P2 以外的任何块是否受到影响?
b. 假设P1的源版本有一点错误。 这个错误通过多少密文块传播? 接收端的作用是什么?
c. 是否可以在 CBC 模式下对多个明文块并行执行加密操作? 解密呢?
d. 假设在使用 CBC 传输的密文块中存在错误,参考下图。 对恢复的明文块产生什么影响?
答:
a. 否。例如,假设 C1 已损坏。输出块 P3 仅取决于输入块 C2 和 C3。
b. P1 中的错误会影响 C1。但由于 C1 是 C2 计算的输入,因此 C2 受到影响。这种影响无限期地持续下去,因此所有密文块都会受到影响。然而,在接收端,解密算法恢复正确的明文块,除了错误的块。您可以通过写出解密方程来证明这一点。因此,该错误仅影响对应的解密明文块
c. 在 CBC 加密中,每个前向密码操作(第一个除外)的输入块取决于前一个前向密码操作的结果,因此前向密码操作不能并行执行。然而,在 CBC 解密中,逆密码函数的输入块(即密文块)是立即可用的,因此可以并行执行多个逆密码操作。
d. 如果在密文块 Ci 的传输中发生错误,则该错误会传播(propagates)到恢复的明文块 Pi 和 Pi+1
对于图 6.3、6.4 和 6.7 中分别显示的每种模式 ECB、CBC、CTR:
a. 如果传输的密文的块 C4 中存在错误,则确定哪些解密的明文块 Px 将被破坏。
b. 假设密文包含N个块,并且P3的源版本有一个位错误,通过多少个密文块来确定这个错误是如何传播的。
Ans:问题假设传输密文的块C4中存在错误。
ECB模式:该模式下,密文块Ci仅作为明文块Pi直接加密的输入。 因此,块 C4 中的传输错误只会破坏解密明文的块 P4。
CBC模式:在这种模式下,当获得明文块Pi和Pi+1时,密文块Ci作为XOR函数的输入。 因此,块 C4 中的传输错误将破坏解密明文的块 P4 和 P5,但不会传播到任何其他块。
CTR 模式:在这种模式下,密文块 Ci 以及加密计数器 ti 仅用作直接解密明文块 Pi 的输入。 因此,块 C4 中的传输错误只会破坏解密明文的块 P4。
是否可以在如图 6.6 所示的 OFB 模式下对多个明文块并行执行加密操作? 解密呢?
Ans: OFB 模式下的加密和解密都可以并行操作。 要看到这一点,请注意在 OFB 中发生的链接只是对 IV 一遍又一遍地重新加密,每次重新加密都与一个明文块进行异或。 因此,如果 IV 已被加密 h 次,则可以并行处理 h 个密文块。 解密也一样
考虑具有以下属性的分组密码算法:
• 输入和输出块长度为 64 位,密钥大小为 56 位
• 给定一个密钥 K,密钥调度需要 2 微秒(2 x 10 -6 秒)
• 密钥调度生成所有子密钥(如果需要)后,加密单个 64 位块需要 0.5 微秒。
计算以下信息:
a. 加密 1MB(2^20 字节)数据所需的总时间(当然以微秒为单位)。
Ans:首先我们需要找到 1MByte 数据中 64 位块的数量为
1MB 中的位数 = 2^20 字节 * 8 位/字节 = 8,388,608 =2^23 位
数据块数 = 8,388,608 / 64 位 = 131,072 个块 = 217 个 64 位块
现在只需认识到密钥 K 将仅为此加密安排一次,并且我们需要加密 131,072 个数据块。
时间 = 2 微秒 + 217 * 0.5 微秒 = 65,536 + 2 = 65,538 微秒
b. 给定 2 个值 C 和 M,使得 C = EK(M) 在未知密钥值 K 下,在单台计算机上破解密码需要多少年(最多)。
Ans : 第二部分寻求破解给定密文C和相关明文M所需的最多时间。为此,需要搜索整个密钥空间。 因为密钥是 56 位长,所以密钥空间是 2^56 = 72,057,594,037,927,936
现在我们知道在找到正确的键之前需要尝试多少个键,我们必须认识到我们只需要测试单个数据块。 然后每次试验都需要密钥安排加上加密/解密的时间(取决于您选择哪一个)。 因此,等式变为 (2^56 (2 微秒 + 0.5 微秒 )) * 0.000001 秒 ~= 1.8x 1011 秒
将此值转换为年 ~= 2,084,999 天 ~=5712 年!!
W4: 数理 Number Theory
考点:IFP,group ring field的概念,费马和欧拉定理 𝝓(n),CRT,原始根,DLP
整数分解问题
b|a 表示a可被b整除(abs(a)>=abs(b))。quotient为商。
质数是数理的中心,只被1和自身整除的数。非质且>1的数称为composite合数。
factor a num分解一个数。factorisation质数分解。
给定一个大正整数n=p·q,找到也都是大正整数且为质数的p和q。
最大公约数
GCD(a,b)表示同时能将a,b整除的最大整数。=1表示ab互质。
Euclidean Algorithm(欧几里得算法,辗转相除法)
就是质数分解之后挑出共有的部分。
群,环,域的概念

群
具有二元运算·的一组元素 G 将 G 中的每个有序元素对 (a,b) 与 G 中的元素 (a·b) 相关联,从而遵守以下公理
- (A1) Closure 闭包:
如果 a 和 b 属于 G,则 a·b 也属于 G
- (A2) Associative 相关:
a·(b·c) = (a·b)·c 对于 G 中的所有 a, b, c
- (A3) Identity element 单位元:
G 中有一个元素 e 使得 a·e = e·a = a 对于 G 中的所有 a
- (A4) Inverse element 逆元素:
对于 G 中的每个 a,在 G 中有一个元素 a’ 使得 aa’ = a’ a = e
- [Abelian Group] (A5) Commutative 交换律:
a·b = b·a 对于所有 a, b 在 G
(ℤ, +) 是群吗?
– (A1) 两个整数之和得到一个整数,即𝑎 + 𝑏 ∈ ℤ 对于任何𝑎,𝑏 ∈ ℤ
– (A2) a + (𝑏 + 𝑐) = (𝑎 + 𝑏) + 𝑐 对于任何整数𝑎, 𝑏, 𝑐 ∈ℤ
– (A3) 0 是关于加法的单位元素
– (A4) 对于任何整数 𝑎 ∈ ℤ,−𝑎 是 𝑎 的逆
其也为Abelian,因为 𝑎 + 𝑏 = 𝑏 + 𝑎 对于任何整数𝑎,𝑏 ∈ ℤ
Rings 环
有时用 {R , + , × } 表示的环 R 是一组元素,有两个二元运算,称为加法addition 和乘法multiplication,这样对于 R 中的所有 a , b , c 都遵守以下公理:
-
[A1-A5]
-
(M1) Closure under multiplication 乘法闭包:如果 a 和 b 属于 R ,则 ab 也在 R 中
-
(M2) 乘法的结合性:对于 R 中的所有 a b c, a(bc) = (ab)c
-
分配法:对于 R 中的所有 a , b , c
- a (b + c) = ab + ac
- (a + b) c = ac + bc
本质上,环是一个集合,我们可以在其中进行加减 [a - b=a + (-b )] 和乘法而不离开该集合
Commutative Ring 可交换环:
• 如果环满足以下附加条件,则称其为可交换环:
▪ (M4) 乘法的交换性:对于R内所有a b, ab = ba
Integral Domain 积分域
积分域是遵循以下公理的交换环。
▪ (M5) 乘法恒等式:对于 R 中的所有 a, R 中有一个元素 e’ 使得 a e’ = e’a = a
▪ (M6) 无零除数:如果 a , b 在 R 中且 ab = 0,则 a = 0 或 b = 0
Field 域
域 F 有时用 {F, +,×} 表示,是一组具有两个二元运算(称为加法和乘法)的元素,因此对于 F 中的所有 a、b、c,都遵循以下公理:
- [A1-M6]
- (M7) 乘法逆:对于 F 中的每个 a,除了 0,在 F 中存在一个元素 使得
• 本质上,域是一个集合,我们可以在不离开集合的情况下进行加、减、乘、除运算。 除法定义如下:
Modular Arithmetic 算术取模
如果a是整数,n是正整数,我们定义模算子“a mod n”为a除以n的余数; 整数 n 称为模数
如果 (a mod n) = (b mod n) ,则两个整数 a 和 b 被称为congruent modulo n (模 n 全等);等价于 a ≡ b(mod n)
b 被称为 a mod n 的余数
– a = qn + b
– 通常选择最小的正余数作为余数
– 过程被称为modulo reduction 模归约
(𝒎𝒐𝒅 𝒏) 运算符将所有整数映射到整数集:{0, 1, … , 𝑛 − 1}
• 我们将ℤ𝑛 = {0, 1, … , 𝑛 − 1} 定义为残差集
• ℤ𝑛 形成一个交换环
注意一些特殊性
• 如果 (𝒂 + 𝒃) ≡ (𝒂 + 𝒄) 𝒎𝒐𝒅 𝒏 那么𝒃 ≡ 𝒄 (𝒎𝒐𝒅 𝒏)
• 但是如果 (𝒂 × 𝒃) ≡ (𝒂 × 𝒄) (𝒎𝒐𝒅 𝒏) 那么 𝒃 ≡ 𝒄 (𝒎𝒐𝒅 𝒏) 仅当𝒂 相对质数于𝒏

Mod 8 Addition
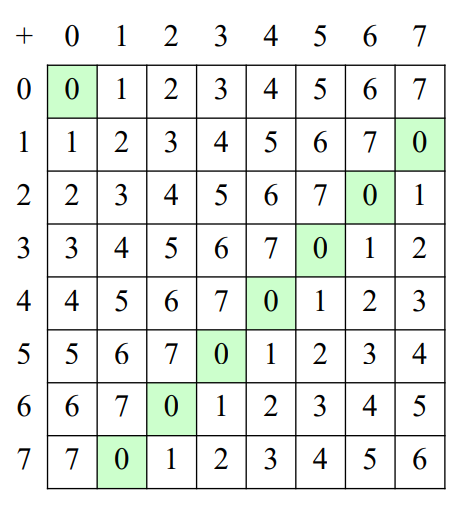
Mod 8 Multiplication

Finite有限/Galois域
有限域在密码学中发挥关键作用
有限域中的元素数必须是素数的幂 (n 为正整数)
也被称为“Galois”域,以纪念首先研究有限域的数学家
• 记为
• 特别是,我们经常使用以下域:
– [本课程最常用的]
–
GF(p) 是整数 {0,1, … , p-1} 的集合,其具有以 p 为模的算术运算,
因为有乘法逆(Zp 中的所有整数都与 p 互质),这些形成一个有限域
因此算术“表现良好”,可以在不离开域 GF(p) 的情况下进行加法、减法、乘法和除法(除了被零除,这是未定义的)
GF(7) Multiplication
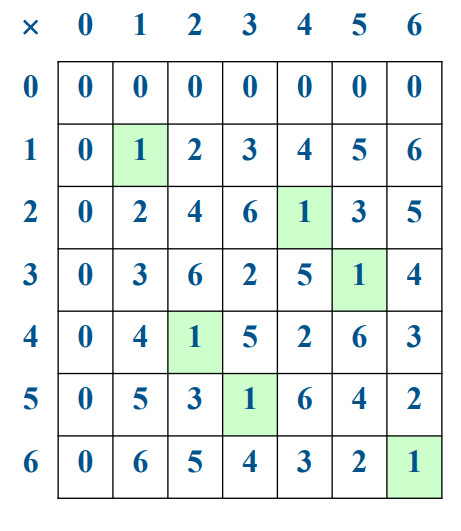
Modular Exponentiation 模幂运算
假设我们要计算 的大值𝒙
• 选项 1:计算 𝒂 ⋅ 𝒂 ⋯ 𝒂 然后 mod n: 非常低效,需要 𝑥 步操作
• 选项2:使用平方乘法算法!非常高效,只需要 操作
平方乘法算法
- 找出最接近 𝒙 的 2 的幂,用 𝒓 表示(不应超过𝑥)
- 计算重复平方模 𝒏 到
- 将 相关幂相乘
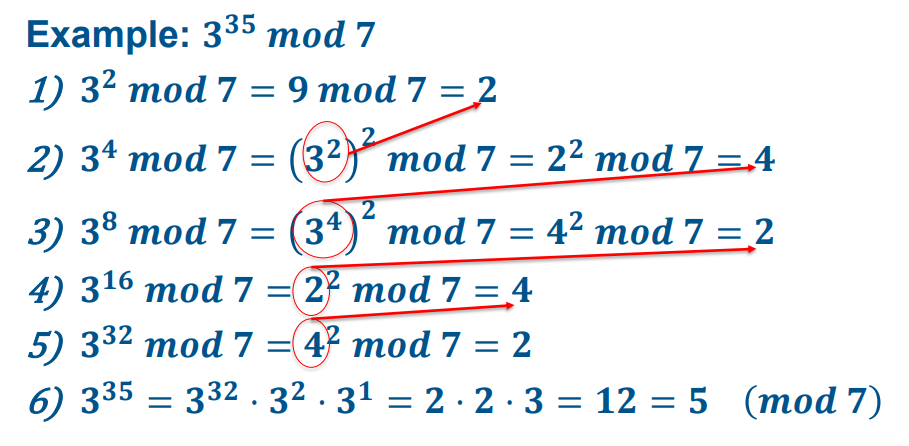
Fermat’s and Euler’s Theorems 费马和欧拉定理 𝝓(n)
费马小定理
•
– 其中 p 是素数
– a 是一个正整数并且
– gcd(a,p)=1
另一种形式是:
在公钥密码学中扮演重要角色
欧拉的 Totient 函数 𝝓(𝒏)
• 做算术取模时 𝑛
• 余数的完整集合是:{0,1, … , 𝑛-1}
• 减少的余数集是那些与 𝑛 相对质数的数字(余数)
– 例如,对于 n=10,
– 完整的余数集是 {0,1,2,3,4,5,6,7,8,9}
– 削减余数集是 {1,3,7,9}
• 削减余数集合中的元素数量 称为欧拉 Totient 函数 𝝓(𝑛)
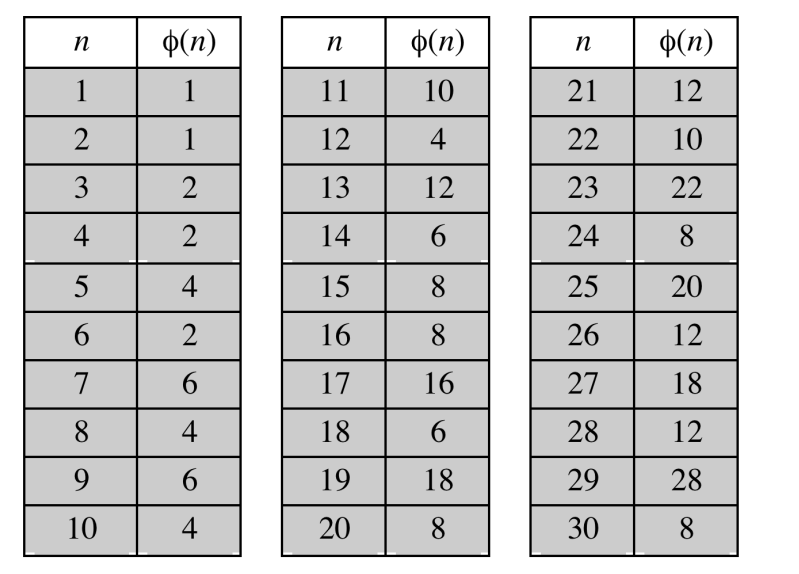
要计算 𝝓(𝑛) 需要计算要排除的余数数量
一般需要质因数分解,但
– 对于 𝑝 (𝑝 质数) :𝝓(𝑝) = 𝑝 − 1
– 对于 𝑝𝑞 (𝑝 和 𝑞 为质数) :𝝓(𝑝𝑞) = (𝑝 − 1)(𝑞 − 1)
例如
𝝓(37) = 36
𝝓(21) = 𝝓(3 × 7) = (3– 1) × (7– 1) = 2 × 6 = 12
欧拉定理
• 费马小定理的推广
• a^{𝝓(n)} = 1 (mod\ n) 对于任何 a,n,其中 gcd(a,n)=1
例如
a=3;n=10; 𝝓(10)=4;因此 = 81 = 1 mod 10
a=2;n=11; 𝝓(11)=10;因此 = 1024 = 1 mod 11
使用欧拉定理求乘法逆: a^{-1} = a^{𝝓(n)-1} mod\ n
中国余数定理 (CRT)
如果 𝑛1, … , 𝑛𝑘 是成对互质,并且如果 𝑎1,…, 𝑎𝑘 是任何整数,则系统:
…
有一个或多个解决方案。
解决方案:
- 得到
- 得到
- 得到 ,其中 $ Y_i * N_i ≡ 1\ mod\ n_ix ≡ a_1 * N_1 ∗ Y_1 + … + a_n * N_n ∗ Y_n\ mod\ N$

Primitive Roots 原始根
原始根
• 从欧拉定理有一个 𝝓(n)mod n=1
• 考虑一个 m=1 (mod n), GCD(a,n)=1
– 存在于 m = 𝝓(n) 但可能更小
– 一旦幂达到 m,循环将重复
• 如果最小的是 m = 𝝓(n) 则 a 称为原始根
• 如果 n 是素数,则原始根的连续幂“生成”所有余数 mod n
• 这些很有用,但相对难以找到
离散对数问题 (DLP)
• 另一个核心密码问题
令𝑮 =< 𝒂 > 是一个cyclic group循环群
DLP:给定𝒂 和随机𝒃 ∈ 𝑮,找到𝒙 使得
由于𝒂 生成𝑮,我们知道一定有这样一个𝒙
在实践中我们要求群的order是大的, 即,
Miller-Rabin Algorithm
通常用于测试大量数字是否为质数
算法是:TEST (n)
- 求整数 k,q,k>0,q为奇数,使得
- 选择一个随机整数a, 1<a<n-1 ;
- if then return (“无结果”);
- 当 j = 0 做 k – 1
- if then return (“无结果”) ;
- 返回(“复合数”)

Tut:
这周是硬核数学题,gcd,质数分解,找余数规律 略
使用以下数字证明费马定理 :
(a) p=5, a=3
(b) p=5, a=4
使用费马定理,求出 。
费马定理指出,如果 p 是素数并且 a 是一个不能被 p 整除的正整数,那么
。因此 。
因此
GF(5)的加法模,乘法模,加法和乘法求逆模

加法逆模 $ -w + w \mod p = 0$
乘法逆模 表示 且也在GF(p)上即 如这里2*3 mod 5 = 1
以多项式形式表示以下十六进制数字:
(a) 1B
1B 二进制:00011011
所以多项式是 x4 + x3 + x + 1
(b) A9
二进制 A9:10101001
所以多项式是 x7 + x5 + x3 + 1
© C2
二进制 C2:11000010
所以多项式是 x7 + x6 + x
(四) 95
9C 二进制:10010101
所以多项式是 x7 + x4 + x2 + 1
反过来多项式转hex略
W5&W6: 非对称加密 Asymmetric Cryptography
副标题是New era of secure communications(加密传输的新纪元)
DSA&ECDSA: 喊我呢?
(其实并没有出现,这俩主要用于数字签名,然而课程专注于的是加密所以是RSA
考点:为啥要公钥?,RSA,高效操作,RSA安全,混合系统;公钥分发,DH 密钥交换协议 和Advanced asymmetric cryptosystem(IBE,ABE),Hash
私有/对称密钥密码的问题
• 要使用私钥密码(例如 DES/AES)进行安全通信,首先必须在发送方和接收方之间共享密钥。问题:如果他们以前从未见过面怎么办?
• 如果爱丽丝希望与 100 个不同的人进行保密通信,她需要保留 100 个不同的密钥(一般而言,𝑛 不同的密钥与 𝑛 不同的各方进行安全通信
• 如果任何密钥被泄露,通信就会受到损害
• 不保护 Alice(发件人)免遭 Marvin(攻击者)伪造消息并声称是 Alice(发件人)发送的
公钥密码系统原理
公钥密码学的概念源于试图解决与对称加密相关的两个最困难的问题:
- Key distribution 密钥分发
- Digital signatures 数字签名
公钥/双密钥/非对称密码术涉及使用两个密钥(一个密钥对):
- 任何人都可能知道的公钥,可用于加密消息和验证签名
- 私钥,仅由所有者拥有,用于解密消息和签署(创建)消息(签名)
- 但是,不是两个独立的Key!
不对称,是因为各方不平等,因为 加密消息 或 验证签名 的人不能分别 解密消息 或 创建签名
理想的功能
• 攻击者无法从公钥中找出私钥(秘密)。
• Alice 和 Bob 无需事先分发共享密钥!
• 每个用户只需要一对公钥和私钥!( Alice 可以用一对钥匙与 100+ 人交流!!
公钥要求(必须满足的条件:
- 一方生成密钥对(公钥,私钥)在计算上很容易
- 发送者 A 知道公钥和要加密的消息,在计算上很容易生成相应的密文,C = E(, M)
- 接收者 B 使用私钥解密生成的密文以恢复原始消息在计算上很容易,D[, E(, M)] = M
- 对于知道公钥 的对手来说,确定私钥 在计算上是不可行的
- 对于知道公钥和密文的对手来说,恢复原始消息 M 在计算上是不可行的
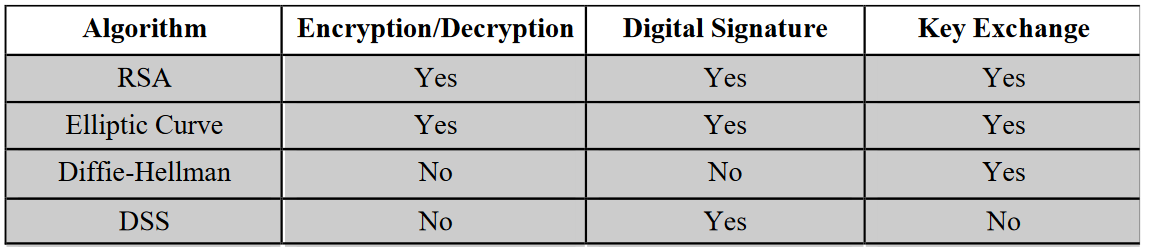
公钥密码系统的应用
• 公钥密码系统可用于:
- Encryption/decryption:
- Digital signature: 发件人用他的私钥“签署”一条消息
- Key exchange: 双方合作交换会话密钥
• 一些算法适用于所有 3 种应用程序,而其他算法只能用于一两个应用程序
单向函数
单向函数是将一个域映射到一个范围,使得每个函数值都有一个唯一的逆函数,条件是函数的计算很容易,而逆函数的计算是不可行的
容易; 不可行(实践中很难)
trap-door(活板门)单向函数是一系列可逆函数 fk,使得
− 容易,如果 k 和 X 已知
− 容易,如果 k 和 Y 已知
− 不可行,如果 Y 已知,但 k 未知
实用的公钥方案取决于合适的trap-door单向函数
如何构建公钥密码系统?
今天的公钥系统依赖于两个基本的数论假设(问题):
- **整数分解问题(IFP)**示例:RSA
- 离散对数问题 (DLP) 示例:Diffie-Hellman (DH) 密钥交换,ElGamal 加密
RSA
它是一种密码,其中明文和密文是 0 到 n – 1 之间的整数,其中某些 n
− n 的典型大小为 2048 位(今天,必须至少使用 2048 位才能获得可靠的安全性
• n 称为 RSA 模数
• RSA 使用带指数的表达式
• 明文以块为单位加密,每个块的二进制值小于某个数 n
• 加密和解密的形式如下,对于一些明文块 M 和密文块 C
• 发送方和接收方都必须知道 n 的值
• 发送者知道 e 的值,只有接收者知道 d 的值
• 这是一种公钥加密算法,公钥为PU={e,n},私钥为PR={d}
Key Generation
选择 p, q p 和 q 都是素数,p ≠ q
计算
计算 𝝓(n) = (p – 1)(q – 1)
选择整数 e: gcd(𝝓(n), e) = 1; 1 < e < 𝝓(n)
计算 d: d ≡ e^{-1}\pmod{𝝓(n)}
简单来说就是(e * d) mod n =1,倒推一个d (e 和 d 的值很大,否则很容易受到蛮力攻击和其他形式的密码分析
公钥 PU = {e, n}
私钥 PR = {d}
Encryption
明文:M < n (消息 m 必须是范围 [1, n] 之间的整数,可以通过将明文分割成小于n的块来实现
密文:
Decryption
密文:C
明文:
证明 RSA 有效
欧拉定理:a^{𝝓(n)} mod n = 1,其中 gcd(a,n)=1
在 RSA 中有:
−
− 𝝓(n)=(p-1)(q-1)
− e \times d =1 \mod 𝝓(n) → e \times d=1+k \times 𝝓(n)对于某个整数 k
• 因此:C^d = (M^e)^d = M^{ed} = M^{1+k𝝓(n)} \\= M^1(M^{𝝓(n)})^k \mod n = M^1*(1)^k \\= M^1 = M \mod n
为了加密长消息,我们可以使用混合密码系统
- 使用非对称密码(如 RSA)就对称密钥达成一致
− 例如,一个用户生成一个随机对称密钥,用另一方的公钥对其进行加密并通过
− 或者双方运行密钥协商协议,例如 Diffie-Hellman 协议(下一讲)
2)使用对称密码(如AES)使用商定的对称密钥在其余部分进行加密
无需事先达成密钥协议!
平方和乘法算法
• 加密和解密都涉及求幂
可以使用平方和乘法算法计算取幂
- 将指数转换为二进制。
- 对第一个1,只需列出数字
- 对于每个随后的0,做平方运算
- 对于每个随后的1,做平方和乘法运算
示例:𝑵𝟑𝟕,仅 7 个步骤

使用公钥高效操作
• 为了加快使用公钥的 RSA 算法的操作,通常对 e 进行特定选择
• 最常见的选择是 65537 ()
• 另外两个流行的选择是 e=3 和 e=17
− 这些选择中的每一个都只有两位 1,因此执行幂运算所需的乘法次数被最小化
− 使用非常小的公钥,例如 e = 3,RSA 变得容易受到简单攻击
− 所以,e=3(甚至 e=17)不是一个安全的选择!
使用私钥高效操作
• 解密使用幂运算为 d 提供幂
− 较小的 d 值容易受到蛮力攻击和其他形式的密码分析
• 可以使用中国剩余定理 (CRT) 来加速解密计算
− 计算和
− 解密𝐶:计算 ; 计算
由于
我们可以通过 𝑀𝑝 & 𝑀𝑞使用 CRT 来找到 𝑀 使得 (比直接快~4 倍
if p=5, q=11, e=3, d=27, C=52 ->
快速计算M:
;
;
得到
$M ≡ 3 \mod 5 $
$M ≡ 2 \mod 11 $
N=pq=55;
N_1=N/5=11;
N_2=55/11=5;
Y1*11 ≡ 1 mod 5; Y1=(1+5*2)/11=1;
Y2*5 ≡ 1 mod 11;Y2=(1+11*4)/5=9;
M ≡ (3*11*1 + 2*5*9) mod 55≡(101)mod 55=13
M = 13
攻击RSA
Brute force
Mathematical attacks: 有几种方法,都等价于对两个素数的乘积进行因式分解
Side-channel attacks, e.g., timing attacks: 这取决于解密算法的运行时间
Hardware fault-based attack: 这涉及在生成数字签名的处理器中引发硬件故障
Chosen ciphertext attacks: 这种类型的攻击利用了 RSA 算法的特性
整数分解问题
• RSA 的安全性严重依赖于整数因式分解问题
• 我们可以从数学上确定 3 种攻击 RSA 的方法:
− 将 n 分解为其两个质因数。 这可以计算 ø(n) = (p – 1) x (q – 1),进而确定 d = e-1 (mod ø(n))
− 直接确定 ø(n) 而不先确定 p 和 q。 同样,这可以确定 d = e-1(mod ø(n))
− 不先确定 ø(n) 直接确定 d
侧信道攻击:定时攻击
• 窥探者可以通过跟踪计算机解密消息所需的时间来确定私钥
• 利用算法运行时间的密钥依赖性
• 示例:平方和乘法算法
- 将指数转换为二进制。
2.对于前1,只需列出数字
3.对于每个随后的0,做平方运算 - 对于每个随后的 1,做平方和乘法运算
• 该攻击不仅适用于 RSA,还适用于其他密码系统
时序攻击对策
常数取幂时间
• 确保所有求幂在返回结果之前花费相同的时间; 这是一个简单的修复,但确实会降低性能
随机延迟
• 通过向取幂算法添加随机延迟以混淆时序攻击,可以获得更好的性能
基于故障的攻击
• 对生成 RSA 数字签名的处理器的攻击
− 通过降低处理器的功率来导致签名计算中的错误
− 故障导致软件产生无效签名,然后攻击者可以分析这些签名以恢复私钥
• 攻击算法涉及引入单位错误并观察结果
• 攻击者需要物理访问目标机器和直接控制处理器输入功率的能力
选择密文攻击 (CCA)
• CCA:对手 Eve 选择一些密文,然后给出相应的明文,用目标的私钥解密
− 假设目标消息是 t,Eve 只知道它的密文 𝐶,𝑤ℎ𝑒𝑟𝑒𝐶 =𝑡𝑒 mod n
− Eve 可以选择 2 作为明文,得到 𝐶𝑎 =2𝑒𝑚𝑜𝑑𝑛,求 𝐶𝑏 =𝐶∗𝐶𝑎 = 2∗𝑡 𝑒𝑚𝑜𝑛的明文
− 给定 𝑚=2∗𝑡,t=m/2
• 为应对此类攻击,RSA Security Inc. 建议使用称为最佳非对称加密填充 (OAEP) 的程序修改明文
私钥密码
• 优势:
- 使用成本低;
- 快;
- 提供低成本硬件芯片
• 弱点
- 密钥分发是个问题
- 安全所需的密钥数量
- 一对用户之间安全通信所需的密钥数量与用户数量成正比
公钥密码
• 优势
- 密钥分发不是问题
- 与 n 个用户通信只需要 2 个密钥
• 弱点
- 使用相对昂贵
- 相对较慢
- 硬件芯片不可用或成本相对较高
Key management
Key
• 用于一对方(人员、系统等)之间对称加密的单个密钥
• 一对密钥(公共和私人)用于您和任何其他人(人、系统)之间的非对称加密。
• 公钥加密有助于解决对称加密的密钥分发问题
– 使用公钥密码术来分发秘密密钥
– 公钥的分发
Distribution of public keys 公钥分发
公钥分发
• 公告
• 公开目录
• 公钥授权和证书
广播
用户将公钥分发给收件人或向整个社区广播
– 例如 将密钥附加到电子邮件或发布到新闻组或电子邮件列表
主要弱点是伪造/制造(伪装、冒充)攻击
– 任何人都可以创建一个声称是其他人的密钥并广播它
– 在发现伪造之前,他们可以伪装成声称的用户
为了防止攻击:
– 在 Bob 为 Alice 加密消息之前,他必须确保他拥有 Alice 的正确公钥(而不是伪造的)。
– Bob 需要一种方法来测试任何将 Alice 的公钥通知给 Bob 的“Alice 的密钥消息”的真实性。
– 除了 Alice 之外,没有人应该能够产生这样的消息,以便它通过 Bob 的测试。
用于实现公钥完整性的一种加密工具是“证书颁发机构”(Certificate Authorities,CA)
公开目录
• 可以通过向公共目录注册密钥来获得更高的安全性
• 目录必须具有以下属性信任:
– 包含 {name, public-key} 条目
– 参与者通过目录安全注册
– 参与者可以随时更换钥匙
– 目录定期发布
– 可以电子方式访问目录
• 公共目录的维护和分发必须由某个受信任的实体或组织负责
• 仍然容易被篡改或伪造
公钥证书
• 证书允许在不实时访问公钥授权的情况下交换密钥
• 证书将身份与公钥绑定,证明公钥的所有权(通常带有其他信息,例如有效期、使用权等
• 所有内容均由受信任的公钥或证书颁发机构 (CA) 签名
• 任何知道证书颁发机构 (CA) 公钥的人都可以验证
• 大多数网络安全应用程序中使用的 X.509 证书
信任链:实际中存在多个Root CA。如果你信任一个Root CA,那么你就会信任它生成的证书
Diffie-Hellman key exchange (DH) 密钥交换
回忆前面提到的混合系统
– 公钥算法很慢
– 我们通常使用对称加密来保护消息内容
– 使用公钥算法共享对称密钥
协商合适的会话密钥的替代方法:Diffie-Hellman (DH) 密钥交换
– 密钥协商方案可以建立一个只有参与者知道的公共密钥
– 依赖于离散对数问题 (DLP)
离散对数问题 (DLP)
• 令𝑮是一个带有生成元𝒈的循环群: 𝐺 =<𝑔>
• DLP:给定𝒈、𝑮和一些𝒉∈𝑮,很难找到𝒙使得𝒈𝒙 =𝒉。
– 一定有这样的𝒙,因为𝐺中的每一个元素都可以写成𝑔的幂
• 可以在任何组中定义 DLP
• 两种著名方案:
- 在 ℤ𝑛 中(更准确地说,是它的一个循环子群)
-> 由于安全要求需要大𝑛
-> 较大的参数 → 效率较低 - 在“椭圆曲线”组中(不就是ECDH) -> 更小的参数→更高效
目前,我们将重点关注ℤ𝒏
所有用户都认可的全局参数:
– 大素数整数(或多项式)p
– g 是 p 的原始根
用户生成自己的密钥
- 选择一个密钥(数字):
-> Alice:𝑎<𝑝
-> Bob:𝑏<𝑝 - 计算并发布他们各自的公钥:
-> Alice:
-> Bob: - 计算共享会话密钥 K
-> Alice:
-> Bob: :
K 在 Alice 和 Bob 之间的对称加密中用作会话密钥
中间人攻击:
由于DH方案中Alice和Bob之间没有身份验证,攻击者可以伪装成Alice/Bob来创建会话密钥并获取Alice和Bob之间的所有通信消息
Hash function
• 哈希函数 H 是一种单向函数,它接受消息 M 并产生固定大小(例如 256 位)的输出(称为消息摘要或哈希值或指纹)
– 很容易为任何消息 M 计算 h=H(M)
• 单向性质:给定 h,找到 x 使得 H(x)=h 在计算上是不可行的
• 抗碰撞性:找到任何一对 (x, y) 使得 H(y)=H(x) 在计算上也不可行
• 确定性:相同的消息总是产生相同的散列
• 哈希函数仅将消息(不需要密钥)作为输入来生成消息摘要
– 任何人都可以计算任何值的哈希值!
• 如果输入仅相差 1 位,则输出将完全不同!
• 可视为确定性伪随机函数(生成随机数)
• 示例包括 MD5、SHA-1、SHA-256 等。
用途
-
常用于创建单向密码文件
- 当用户输入密码时,将该密码的哈希值与存储的哈希值进行比较以进行验证
- 大多数操作系统都使用这种密码保护方法
-
可用于入侵和病毒检测
- 为系统上的每个文件存储 H(F) 并保护散列值
- 稍后可以通过重新计算 H(F) 来确定文件是否已被修改
- 入侵者需要在不改变 H(F) 的情况下改变 F
-
可用于构造伪随机函数 (PRF) 或伪随机数生成器 (PRNG)
- 基于散列的 PRF 的一个常见应用是生成对称密钥
要求和安全
原像(Preimage)
• x 是哈希值 h 的原像 h = H(x) 是一个数据块,其哈希函数,使用函数 H,是 h
• 因为 H 是多对一映射,对于任何给定的哈希值 h,通常会有多个原像Preimage碰撞
• 在我们有 x ≠ y 且 H(x) = H(y) 时发生
• 因为我们使用散列函数来保证数据完整性,所以冲突显然是不可取的
攻击
- Brute-Force Attacks
- Cryptanalysis (MD5 and SHA-1 are broken by cryptanalysis,)
Birthday Attacks
• “如果有 23 人的房间,他们的生日完全随机,则该房间中的任何 2 个人有 50 到 50 次生日相同的机会”
• 生日悖论:如果你从一组𝑁元素中随机选择大约 𝑁元素,你很可能会选择相同的元素两次
• 生日攻击:对手希望找到两个产生相同哈希函数的消息或数据块
• 生日攻击的工作原理:
- 随机生成一系列明文X1,X2…
- 对每个Xi计算hash测试是否存在相同
- 当碰撞就停
Advanced asymmetric cryptosystems
传统的公钥密码学需要一个基础设施(有CA的存在)来确保公钥的真实性
• 它还需要昂贵的通信和计算(获取证书 + 验证证书)
• 不需要这种昂贵过程的新密码系统——基于身份的加密 (IBE)
Identity Based Encryption (IBE) 基于身份的加密
• IBE,每个用户都由一个身份代表——可以是电子邮件地址、姓名、身份证号码等。
• 加密只需要收件人的身份(例如电子邮件地址)
• 私钥生成器 (PKG),受信任的第 3 方,发布所有用户的私钥
• 不需要公钥或证书!
系统设置过程:PKG 生成自己的主密钥 (msk) 和主公钥 (mpk)
– msk 只有 PKG 知道
– mpk 作为公共参数发布
密钥生成过程:
- 用户去PKG(带有一些带照片的ID或物理文件,其中包含用户的身份作为物理认证过程)
- PKG 使用其 msk 为该用户生成与用户身份相关联的用户密钥。
加密过程:
- 发送方只需要知道接收方的身份(以及系统参数mpk)
- 发送者从(m, ID, mpk)生成密文,其中m为明文消息,ID为接收者身份,mpk为系统参数
解密过程:
- 接收者使用他/她的用户密钥来解密密文
安全性:
– 如果密文是为 [email protected] 加密的,除了与 [email protected] 关联的密钥的所有者之外,没有人可以解密此密文
– 这里不存在PKI(无证书)中的伪造攻击! -> Marvin 无法从 PKG 获取私钥
IBE 需要一个称为双线性配对的数学函数(基于椭圆曲线)
• 它是两组之间的单向映射函数:G 和 GT,使得 G 和 GT 中的离散对数很难
• 表示为一个映射
它取 G 组中的两个元素并输出 组中的一个元素
双线性配对
• 假设是具有群序的生成器(即,具有个元素:)
• 我们有以下属性:
– Bilinear双线性:, 对于
– Non-degenerate 非退化:
第一个实用的 IBE 方案是由 Dan Boneh 和 Matthew K. Franklin 在 2001 年(我们称之为 Boneh-Franklin 计划)
设置:
– 双线性配对 群序为 p
– g 是 G 中的生成器
– PKG 选择 作为主密钥
– PKG 计算 作为主公钥(mpk)
– 选择两个哈希函数:
->
-> 对于一些固定的 n
– 输出系统参数:{e, G, GT, K, H1, H2}
密钥生成:
为一个 ,发布一个密钥PKG 计算:
- 用户密钥$d_{ID}=(Q_{ID})^s $, 该密钥以𝐼𝐷身份提供给用户
加密
给定一个消息,以及一个身份, 计算:
- 选择一个随机数
- 计算, K 即 mpk
- 计算
解密
给定 , 可以使用与 𝐼𝐷 关联的密钥检索明文:
• 由于 ,我们只需要验证是否?
• 回忆:
– PKG 的公钥𝐾 =𝑔𝑠
– Alice 的密钥
– 密文
– 𝑇𝐼𝐷 =𝑒(𝑄𝐼𝐷,𝐾)
正确性:
IBE 消除了证书的使用, 然而,它仍然是一对一的加密
– 即,每个密文的目标是由单方解密
• 是否可以进行一对多加密?
– 广播加密
– 基于属性的加密 (ABE)
Attribute Based Encryption (ABE) 基于属性的加密
• 1 个权限和具有不同属性的用户
• 属性可以是:
– {男,学生,计算机科学,莫纳什大学}
– {女性,会计师,ABC 公司}
– {日本人,1980-1989 年间出生,博士}
• 用户通过他/她的属性来识别,而不是公钥或身份
• 用户根据他/她的属性从权限获取密钥
• 用户是否可以根据他/她的属性是否满足访问策略来解密密文,例如
– { 学生 AND 计算机科学 AND 莫纳什大学}
基于属性的加密 (ABE) 2 种类型:
- 密钥策略 ABE (KP-ABE)
-> 根据访问策略生成用户的密钥
-> 数据使用一组属性加密 - 密文策略 ABE (CP-ABE)
-> 用户的密钥是通过一组属性生成的
-> 数据使用访问策略加密
特性
• 一对多
• 公共参数、加密/解密复杂度、密钥大小、密文大小都与用户(解密者)数量无关
• 加密者不需要知道解密者的身份(只需设置策略)
• 如果有很多用户(例如一家公司有 100 万员工),优势将非常显着
Tut:
在 RSA 密钥生成中,为什么我们需要 gcd(e,ø(n))=1?
如果 gcd(e,ø(n)) 不等于 1,则不可能找到整数 d 使得 d.e =1 mod φ(n)
使用 RSA 算法,其中:
p 和 q 是素数,n = p q
φ(n) = (p-1)(q-1) 而 ed mod φ(n) = 1
密文 C = Me mod n 和明文 M = Cd mod n
(e,n) 和 (d,n) 分别是公钥和私钥
对以下内容进行加解密
(a) p=3, q=11, e = 7, M = 5
n = p × q = 33; e = 7; M = 5; φ(n) = 2 × 10 = 20; e × d mod 20 = 1; hence d = 3
Encryption:
C = M^e mod n = 5^7 mod 33 = 14
Decryption
M = C^d mod n = 14^3 mod 33 = 5 = M
在使用 RSA 的公钥密码系统中,您截获发送给公钥为 e = 5, n = 35 的用户的密文 C = 10。明文 M 是什么?
n = 35 = 7 × 5; φ(n) = 6 × 4 = 24
e × d mod 24= 1; d = 5
M = C^d mod n = 10^5 mod 35 = 5 = 5 mod 35
假设我们有一组用 RSA 算法编码的块,但我们没有私钥。假设 n = p × q,e 是公钥。假设还有人告诉我们他们知道其中一个明文块与 n 有一个公因子。这对我们有任何帮助吗?
假设 M = kp(即明文块 M 与 n 有一个公因子,这意味着它有 p 或 q 作为其因子之一,我们知道 M < n 所以它不能同时是 p 和 q,我们假设它是 p 并且同样的论点也适用于 q)。
C = Me mod n = (kp)e mod pq = kepe mod pq = r
其中 r 是除法 kepe 的余数
r = kepe − xpq 对于某些 x 作为商所以 r = p(kepe−1 − xq) pq
所以余数有 p 作为它的因数之一,或者 r 是素数,在这种情况下它只能是 p 或者它是合数,在这种情况下,r 很可能有小素数,所以用小素数试除我们可以轻松分解 r 并获得 p(使用素性检验)并使用它分解 n 并获得 q 并使用 p 和 q 计算 φ(n) 然后 d
为了避免这种情况,我们可以为 M 选择合适的块大小,使得 M < p 和 M < q 并且由于 p 和 q 是素数,那么 GCD(M, p) = 1 和 GCD(M, q) = 1。例如,使用 1024 位 RSA 密钥,我们可以使用任何小于 512 位的块大小。
假设 Bob 使用具有非常大模数 n 的 RSA 密码系统,在合理的时间内无法找到因式分解。 假设 Alice 向 Bob 发送一条消息,将每个字母字符表示为 0 到 25 之间的整数(A ← 0, . . ., Z ← 25),然后使用具有大 e 和大 n 的 RSA 分别加密每个数字。 这种方法安全吗? 如果不是,请描述针对此加密方法的最有效攻击
考虑一组字母字符{A, B, . . ., Z}。 对应的整数,代表每个字母字符在字母表中的位置,形成一组消息块值SM={0, 1,2, . . ., 25}。
对应的密文块值集合 SC ={0^e mod n, 1^e mod n, . . ., 25^e mod n},每个人都可以在知道 Bob 的公钥的情况下计算出来。 因此,针对问题中描述的方案最有效的攻击是计算 M 的所有可能值的 Me mod n,然后创建一个以密文作为索引的查找表,以及相应的明文作为适当的值 表中的位置。
CRT RSA:在RSA密码方案中,使用了三个n位数字,公共模数n、公钥e和私钥d。 设 n = p ⋅ q 其中 p, q 是秘密素数。 还让 e ⋅ d = 1 mod(p − 1)(q − 1)。
假设 m 是要加密的消息(明文),RSA 加密的结果(密文)是 c = m𝑒 mod n,解密的结果是 m = cd modN。 CRT 通常用于 RSA 解密,因为私钥 d 的位长必然很长。 在 CRT RSA 中,我们计算 S𝑝 = cdp modp 和 𝑆𝑞 = 𝑐𝑑𝑞 𝑚𝑜𝑑𝑞,其中 𝑑𝑝 = 𝑑 𝑚𝑜𝑑 (𝑝𝑑 (𝑝) -1)。 然后,根据我们在中国剩余定理中遵循的高斯组合算法计算最终结果
CRT:
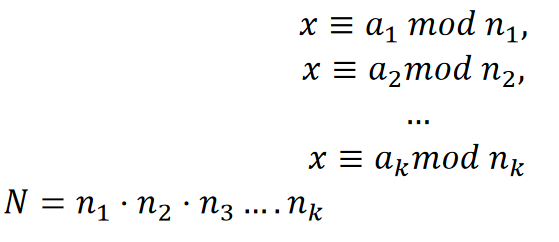
转为
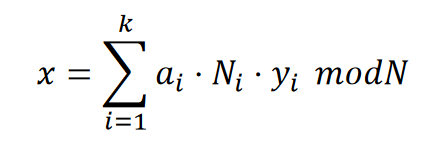
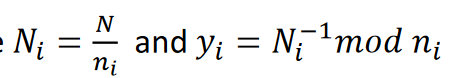
鉴于上述情况,假设公钥为 e=3,私钥为 d=27,则使用 CRT RSA 解密密文 c=52,其中 n=55 p=5 和 q=11。
为了使用 CRT 计算 RSA 结果,我们有两个 ai:Mp 和 Mq 以及两个ni: n1=p 和 n2=q
因此 CRT 重建公式变为
N1 = N/n1 = (p·q)/p = q; N2=N/n2= (p·q)/q = p
y1=N1^-1 mod n1 = q^-1 mod p; y2 = N2^-1 mod n2 = p^-1 mod q
则
for k=2
要找到 𝑞−1𝑚𝑜𝑑𝑝,我们需要解方程
$𝑞 ⋅ 𝑞^{−1}𝑚𝑜𝑑𝑝 = 1 → 11 ⋅ 𝑞^{−1}𝑚𝑜𝑑5这可以很容易地发现是 $$𝑞^{−1} = 1$
为了找到 𝑝−1𝑚𝑜𝑑𝑞 我们需要解方程
𝑝 ⋅ 𝑝−1𝑚𝑜𝑑𝑞 = 1 → 5 ⋅ 𝑝−1𝑚𝑜𝑑11这可以被发现是
𝑀 = (𝑀𝑝 ⋅ 𝑞 ⋅ 𝑦1 + 𝑀𝑞 ⋅ 𝑝 ⋅ 𝑦2)𝑚𝑜𝑑𝑛 = (3 ⋅ 11 ⋅ 1 + 2 ⋅ 5 ⋅ 9)𝑚𝑜𝑑55 == (33 + 90)𝑚𝑜𝑑55 = 123𝑚𝑜𝑑55 = 13
Mid term
比较简单,全选择题,时间足够
W7&8: 数字签名 Digital Signature
考试来了。W7是考试。
BTC: 老本行了
考点:基础签名方案(RSA,schnorr),高级(Threshold,Aggregate,区别),匿名(Group,Ring,区别,Linkable Ring);5个Attack模型,4个伪造方式,RSA上的Attack,Blind签名;ECDLP,为什么ECC的密钥长度比RSA和DH短?,椭圆曲线上的点加法,标量乘法,ECDSA
数字签名
用途
- 对等实体(Peer entity)身份验证:验证用户的身份
- 数据源认证: 验证数据来源
- 数据的完整性:确保收到的数据是由授权实体发送的
- 不可否认性:防止通信中的一方否认
要求
- 必须取决于签名的消息: 消息无法替换
- 必须使用发起者(发送者)独有的信息
– 防止伪造和否认 - 必须相对容易生产和验证
- 在计算上无法伪造
– 现有数字签名的新消息
– 对给定消息使用欺诈性数字签名 - 将数字签名保存在存储中是切实可行的
直接数字签名 Direct Digital Signature
指仅涉及通信方的数字签名方案
- 假设目标知道源的公钥
- 可以通过使用共享密钥加密整个消息和签名来提供机密性
- 首先执行签名功能,然后执行外部机密功能很重要
– 如有争议,某些第三方必须查看消息及其签名 - 方案的有效性取决于发送方私钥的安全性
– 如果发件人稍后希望拒绝发送特定消息,则发件人可以声称私钥丢失或被盗,并且其他人伪造了他或她的签名
– 阻止或至少削弱这种策略的一种方法是要求每条签名消息都包含时间戳,并要求将泄露的密钥迅速报告给中央机构
步骤:
• 设置和密钥生成:假设签名者是 Bob
– 准备一对公钥和私钥/私钥
– 发布公钥
– 保留密钥
• 签名:使用密钥对文档进行签名
– 文件和签名对是 Bob 已签署文件的证明。
• 验证:任何一方都可以通过使用 Bob 的公钥来验证这对文档和签名
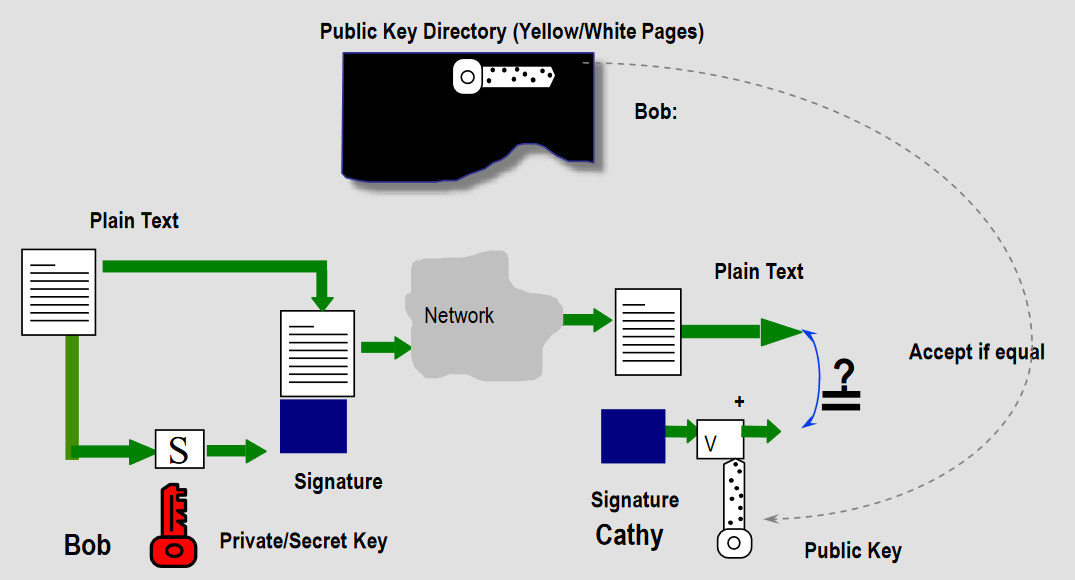
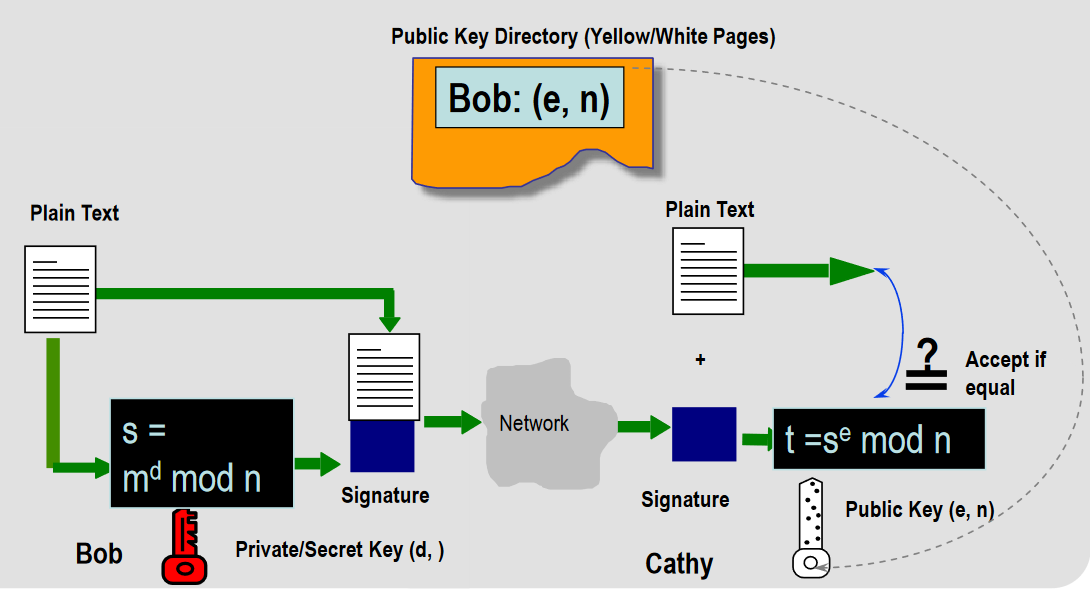
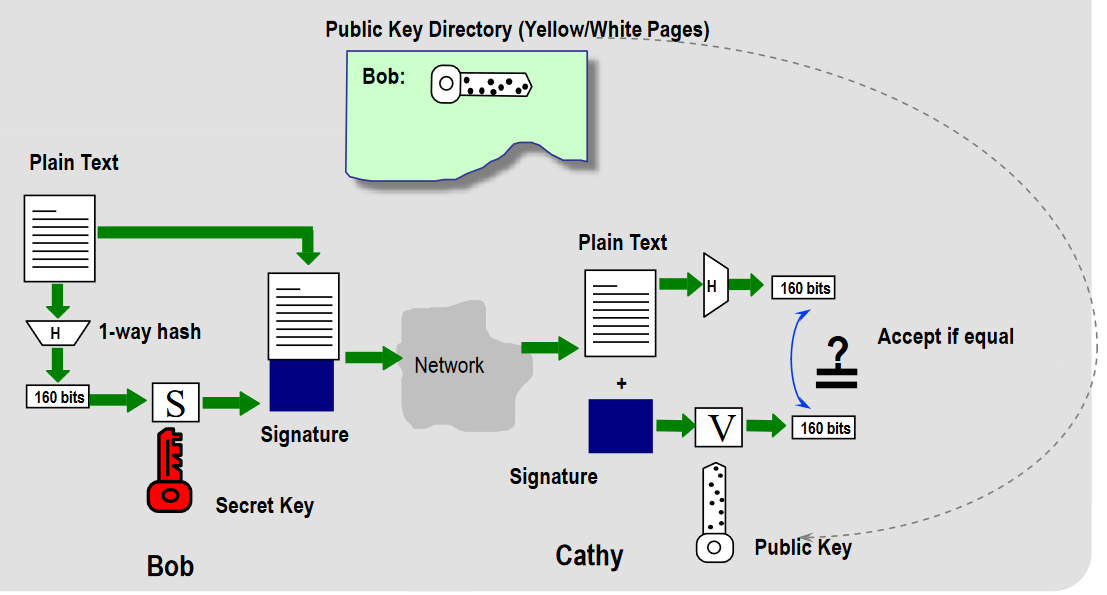
优点:
- 不可伪造
— 需要10亿年才能刻意伪造一个签名! - 签字人不可否认
- 普遍可验证
- 文档不同而签名不同
- 易于实现
– 纯软件 或
– 纯硬件 或
– 软件 + 硬件
Schnorr 签名方案
• 基于 DL 的签名方案
• 设置:
– 定义一个质数阶为 q 的群 G,生成器为 g,其中假设离散对数问题是困难的。
– 定义一个哈希函数𝐻:0,1 ∗ → 𝑍𝑞
• 密钥生成:
– 用户选择一个秘密密钥 𝑥 ∈ 𝑍𝑞 并计算公钥 𝑦 = 𝑔^𝑥
签名:使用密钥 x 对消息 m 进行签名:
- 随机选择
- 计算
- 计算
- 计算 𝒔 = 𝒌 − 𝒙𝒆 mod q
- 输出签名𝜎 = (𝒔, 𝒆)
验证:使用公钥 (𝒚, 𝒈) 验证签名 𝜎 = (𝒔, 𝒆) :
- 计算
- 计算
- 如果 e=e’,则输出有效。 否则输出无效
高级签名方案
如果消息来自一个组,谁签名?
• 信任一个人签字是很危险的
• 签名者可能会修改文档
如果每个用户使用他/她的密钥对消息进行一次签名
– Bob 必须验证消息 N 次
因此我们需要高级的签名方案处理这类问题
- Threshold Signature 阈值签名
– 至少有 n 个签名者,对应 到一个公钥,在一条消息上
– 需要一个“领导者”在 n 个签名者之间分发密钥 - Aggregate Signature 聚合签名
– n 个签名者,对应 n 个不同的公钥,在 n 个不同的消息上签名 - 都仅验证一次!
Threshold Signature
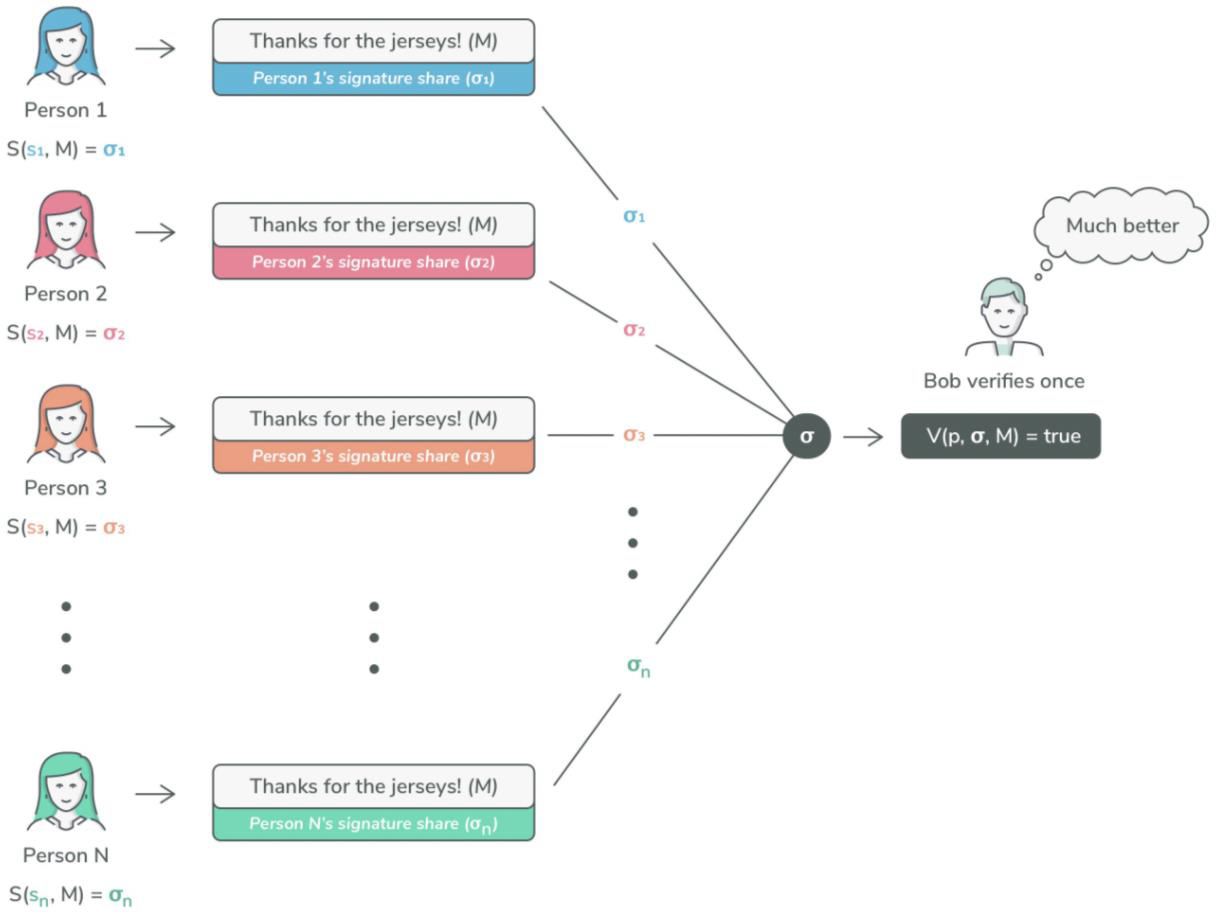
Aggregate Signature(就是这次BTC taproot升级带来的schnorr支持的功能
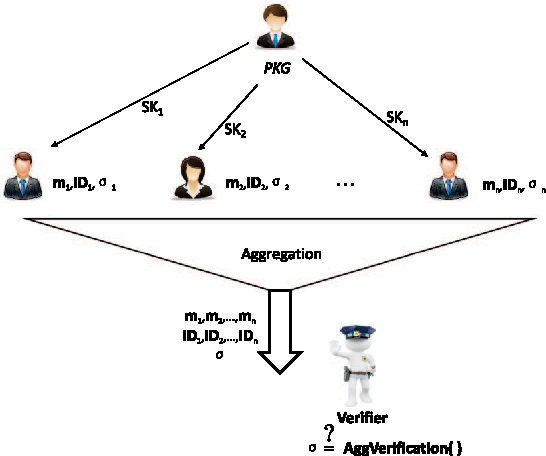
匿名签名 Anonymous Signature
- 组签名 Group Signature:
– 允许群组成员代表群组匿名签署消息 - 环签名 Ring Signature:
组签名
• 有一个组长 (GM)
• 设置
– GM 生成 GM 私钥和组公钥
• 如何加入群组?
– 联系GM
– GM 为用户颁发私钥(注意:没有个人公钥!)
• 签名(代表小组)
– 用户使用他的私钥对消息进行签名
• 验证:任何人都可以使用组公钥验证签名,并且:
– 确认签名者是组内的用户之一
– 不知道真正的签名者是谁
• 开放
– GM可以撤销匿名!
– 无条件 GM 只使用他的 GM 私钥,他可以计算任何签名的实际签名者是谁
总结:
• 匿名签名
• 没有人(除了 GM)知道实际签名者是谁/链接任何两个签名
• 只能确认签名者在组内
• 组经理职责:
– 组的形成(组pk
– 发行个人私钥
– 撤销或公开匿名(对任何行为不端的用户)
• 需要信任 GM
环签名
也是一种匿名签名,– 验证者只知道签名者是组中的用户之一,但不知道谁是真正的签名者
• 环签名和群签名的区别
– 没有组经理GM
– 每个用户生成他/她自己的私钥/公钥对,就像一个普通的公钥密码系统
• 如何组建/加入小组?
– 只需包含其他人的公钥!
– 特设小组(Ad hoc group)自发
• 如何撤销/开放匿名?不可能的!
– 没有人(真实签名者除外)可以计算/找出实际签名者是谁
– 甚至无法检测两个签名是由同一签名者还是不同签名者生成的(不可链接性)
• 设置:(与 Schnorr 签名相同)
– 签名方案的所有用户都同意质数阶为 q 的群 G 与生成器 g ,其中假设离散对数问题是困难的。
– 定义一个哈希函数
• 密钥生成:(与 Schnorr 签名相同)
– 用户选择一个私钥并计算公钥
签名
– 实际签名者通过包含他们的公钥**(假设组/环中有 n 个用户)**来选择一组用户(以形成组)
– 让实际签名者的索引为 𝝅
– 要签署消息 m,请执行以下步骤:
- 随机选择
- 计算 c_{𝝅+1} = H(Y,m,g^u)
- 对于,随机选择 并计算
- 计算
– 签名是
验证:在输入时 ( 𝒀, 𝒎, 𝝈),
- 对于 计算
然后 如果 - 检查是否. 如果是,接受。 否则,拒绝。
这个想法是为了证明签名者知道 n 个公钥中的秘密密钥 (DL) 之一。
可链接的环签名
• 普通环签名不可链接
– 没有人可以检测两个签名是否由同一签名者生成
• 在某些情况下,这种“匿名性”可能太强了,例如 投票
• 可链接性是一个不错的选择!
– 任何人都知道两个签名是否由同一签名者生成
– 然而没有人知道真正的签名者是谁
• 设置
– 与(正常)环签名相同
• 密钥生成
– 与(正常)环签名相同
• 标志
– 首先设计可链接的级别:群组链接 Group Linkable,事件链接 Event Linkable,一次性链接One time Linkable
签名:假设是事件可链接的
- 计算 和链接标签
- 随机选择
- 计算 c_{𝝅+1} = H(\textcolor{red}{event},Y,m,g^u, \textcolor{red}{h^u})
4.对于$ i=\pi +1,…,n,1,…,\pi−1$,随机选择 并计算 - 计算
– 签名是
验证: 当输入 ( 𝑒𝑣𝑒𝑛𝑡,𝒀,𝒎,𝝈),
- 对于,计算
; 然后 - 检查是否 。如果是,则接受。否则,拒绝。
关联
– 检查链接标签 是否相同
这个想法是为了证明签名者知道 n 个公钥中的一个秘密密钥 (DL) 并且 已知 私有密钥 等于 到基数h的DL(回忆: 且 以及 )
攻击
攻击模型
Key only 攻击:C 只知道 A 的公钥
Known message 已知消息攻击:C 被授予访问一组消息及其签名的权限
Generic chosen message 通用选择消息攻击:C 在尝试破解 A 的签名方案之前选择一个消息列表,与 A 的公钥无关; C 然后从 A 获得所选的有效签名
Directed chosen message 定向选择消息攻击:类似于通用攻击,不同之处在于要签名的消息列表是在 C 知道 A 的公钥之后但在看到任何签名之前选择的
Adaptive chosen message自适应选择消息攻击:C 可以从 A 请求依赖于先前获得的消息签名对的消息签名
伪造 Forgeries
Total break 整体截断: C 确定 A 的私钥
Universal forgery 通用伪造: C 找到了一种有效的签名算法,该算法提供了在任意消息上构造签名的等效方法
Selective forgery 可选伪造: C 为 C 选择的特定消息伪造签名
Existential forgery 既存伪造: C 为至少一条消息伪造签名;但是C 无法控制消息
椭圆曲线
为什么是椭圆曲线密码术?
• 较短的密钥长度
• 计算复杂度较低
• 低功耗要求
• 更安全
介绍
• 让p > 3 为素数。上的椭圆曲线 是同余解的集合
其中 , , 是常数使得
0 (mod p),连同一个特殊的点 O 称为无穷远点
椭圆曲线的特点
– 形成一个阿贝尔群 abelian group
– 关于 x 轴对称
– 指向无穷大作为单位元素:P+O=P
密码学椭圆曲线例子:在 上的
则我们有一个有 13 个点的组(包括无穷远 O 处的点)
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | 8 | 5 | 3 | 8 | 4 | 8 | 4 | 9 | 7 | 4 | |
| QR? | N | N | Y | Y | N | Y | N | Y | Y | N | Y |
| Y | 4,7 | 5,6 | 2,9 | 2,9 | 3,8 | 2,9 |
ECC计算
• 加点
– 添加位于椭圆曲线上的两个点 – 导致曲线上的第三个点
• 标量乘法
– 点乘法是重复加法
– 如果 P 是曲线上的已知点(又名基点;域参数的一部分),Q=kP 是 P + P + P + P… +P 相加的运算(k 次,k 是标量)
– Q 是生成的公钥,k 是公钥-私钥对中的私钥
• 在曲线上添加两个点
• P 和 Q 相加得到 P+Q,它是 R 沿 X 轴的反射
• 延长 P 处的切线以在一点处切割曲线; 它的反射是2P
• P 和 2P 相加得到 3P
• 同样,可以根据需要多次执行此类操作以获得 Q = kP
ECC 中的离散对数问题
• ECC 中的 DLP:如果 Q=kP,给定 P 和 Q,很难得到 k
• 解决方法包括:蛮力攻击, Pollard’s Rho攻击(两者在计算上都是昂贵的或不可行的
• 适用于 ECC 的版本称为椭圆曲线离散对数问题 (ECDLP , Elliptic Curve Discrete Log Problem)
ECDSA
Elliptic Curve Schemes
• Elliptic Curve Digital Signature Algorithm (ECDSA)

ECDSA签名
- 选择一个随机数k,1≤k≤n-1
- 计算 kG = (x1, y1)
- 计算 r = x1 mod n
- 计算 k-1 mod q
- e = Hash(m) 其中 m 是要签名的消息
我们的签名为 (r, s)
注意 e 不能长于 n。 如果是这样,只有e的最左边的位是有符号的,其中𝐿#是n的位长
ECDSA验证
- 验证 r 和 s 是否属于区间 [1, n-1] 以使签名有效。
- 计算 e = Hash(m)
- 计算
- 计算 u1 = ew mod n 和 u2 = rw mod n
- 计算 (x1,y1) = u1G + u2Q。
- r = x1 mod n 时签名有效,否则无效
Tut
文字题
W9: Lightweight Security
超乎想象的内容,原以为只是介绍,没想到内容和算法都挺多
考点:TMD tradeoff attack,流密码上的TMD,在/离线签名,在/离线加密
Lightweight Security研究在资源受限环境下的安全性
• 轻量级密码学
• 验证:轻量级身份验证协议 Lightweight authentication protocols ; 轻量级密钥协商协议 Lightweight key agreement protocols
• 保密:轻量级块/流密码 Lightweight block/stream cipher ; 轻量级认证加密 Lightweight authenticated encryption
• 完整性:轻量级消息身份验证代码 Lightweight message authentication codes (MACs)
区别:
• 迄今为止,我们看到的传统算法并非为资源受限的设备量身定制
• 不是 RSA
• 不是 Diffie-Hellman
• 甚至不是 AES(它已经比 RSA/Diffie-Hellman 高效得多)
• 如果我们不做好研究,事情就会出错……
• 工业与学术
案例: 1. KeeLoq 2. Mifare …
好的算法:
学术界对过去十年开发的轻量级算法进行了大量研究
轻量级分组密码:
• PRINCE – Asiacrypt 2012
• Midori – Asiacrypt 2015
• SIMECK – CHES 2015
• 还有很多…
轻量级流密码:
• Sprout – Fast Software Encryption (FSE) 2015
• Plantlet – Transactions On Symmetric Cryptology 2017
• Lizard – Transactions On Symmetric Cryptology 2017
• 仅此而已!
为什么有这么多块密码而不是流密码?时间/内存/数据 权衡 TIME/MEMORY/DATA (TMD) TRADEOFF 攻击!
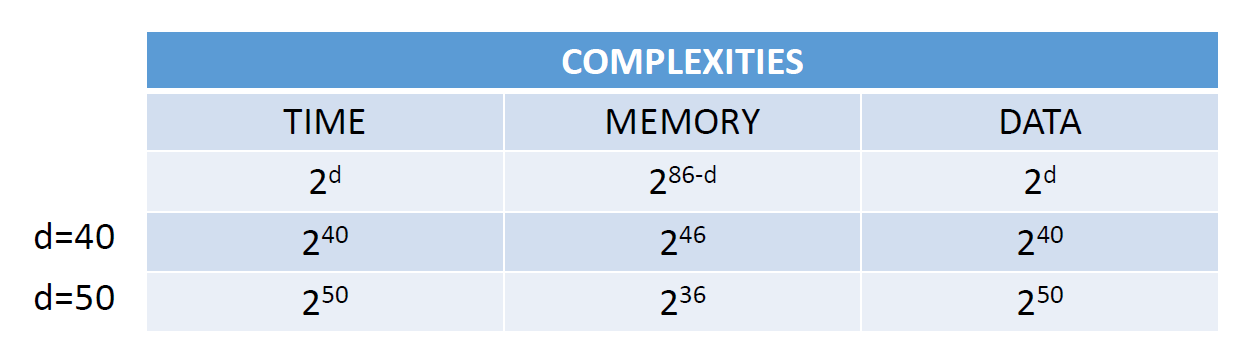
在这种情况下,我们可以以时间和数据为代价来降低内存复杂性。 但是,我们不能一起降低所有的(T&M&D)复杂性!
TMD 权衡攻击
两个极端:
• 蛮力:实时(在线)尝试所有可能性并找到正确的可能性。
• T = N
• P ≈ M ≈ D ≈ 0
• 完整词典:预先计算所有可能性并将它们放在(排序的)表中。 只需实时查找正确的候选即可。
• P = M = N
• T ≈ D ≈ 0
| 注解 | 含义 |
|---|---|
| N | 搜索空间大小 |
| T | 在线阶段所需时间 |
| P | 预计算阶段所需时间 |
| M | 所需的内存量 |
| D | 可用的在线数据量 |
攻击分为两个阶段:
预计算(离线)阶段:
• 此时的攻击者无法访问实时(在线)数据。所以,目前还没有目标密文。
• 此阶段仅针对所有可能要攻击的目标执行一次!
• 因此,该阶段的时间复杂度相对较小。
在线阶段(实时):
• 现在,攻击者拥有使用未知密钥加密的实时数据。
• 必须对每个目标重复此阶段!
• 因此,在线时间复杂度非常重要!
例如:
攻击 I:• 离线阶段需要 1 个月。• 在线阶段需要 1 分钟。
攻击 II:• 离线阶段需要 1 天。• 在线阶段需要 1 天。
当破解 100 个密文
• 使用攻击 I:1 个月 + 100 分钟 = ~30 天
• 使用攻击 II:1 天 + 100 天 = 101 天
当破解 1000 个密文
• 攻击 I:1 个月 + 1000 分钟 = ~31 天
• 使用攻击 II:1 天 + 1000 天 = 1001 天
密钥流生成器
• 正如我们之前所见,流密码的工作原理如下:
𝐶 = 𝑀⊕𝐾
其中 𝐾 是密钥流,𝑀 是要加密的明文。
• 攻击者的目标可能是恢复给定一部分的所有密钥流序列。
• 结果,分析简化为密钥流生成器(生成𝐾的算法)的分析。
对 流密码 的 Babbage-Golic 权衡攻击
• 假设攻击者可以访问密钥流的一部分。
• 攻击者的目标是恢复正确的内部状态。
• 请注意,状态更新中没有使用密钥。
• 一旦内部状态恢复,您就可以生成整个密钥流。
• N=2s,其中s 是内部状态大小。
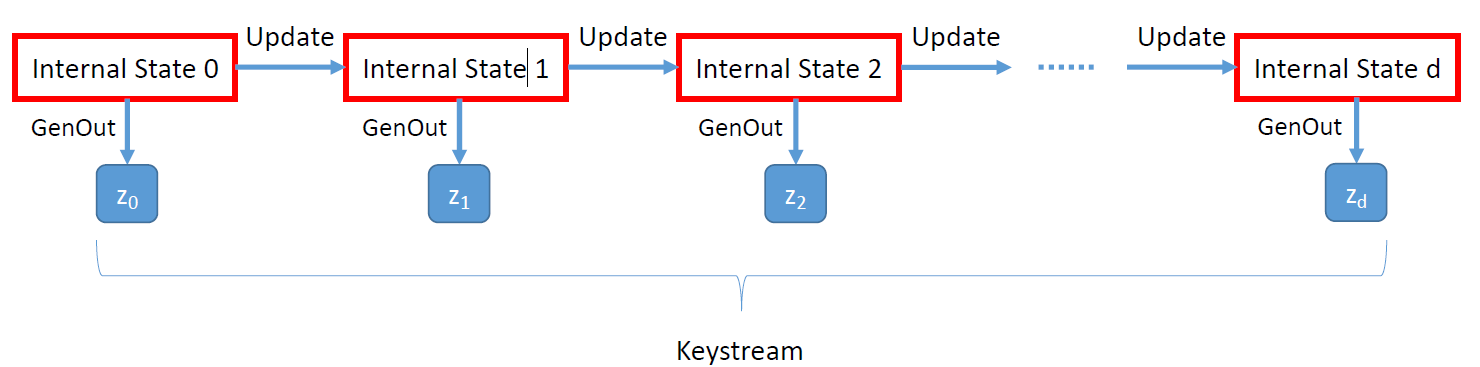
预计算(离线)阶段
• 取 M 个随机内部状态 S1,…,SM
• 计算 s 位对应的密钥流 Zi
• 将 (Si,Zi) 对存储在根据 Zi 排序的表中
在线阶段
• 取大约 D 位的密钥流
• 将其分成 D 个 s 位的块(通过重叠)
• 搜索表中的每个密钥流块
• 如果找到匹配项,则表中对应的内部状态是正确的内部状态
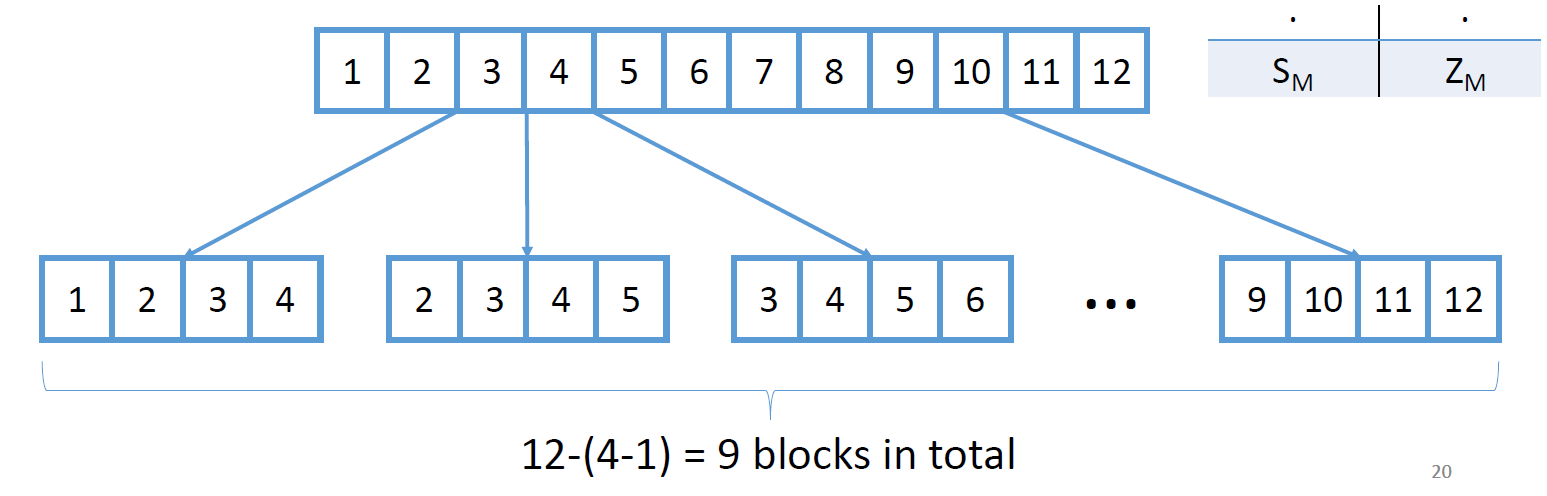
切割密钥流keystream
假设我们总共有 12 位并且想要将其分成 4 位的块
复杂度
• 根据生日悖论,如果 D*M = N,则匹配很可能在在线阶段被发现。
• T = D 因为我们在在线阶段总共使用 D 个块。
• P = M 因为我们在离线阶段总共使用 M 个块。
• 从这里开始,T*M = N。
• 我们可以通过设置来最小化所有的复杂性
其中 s 是内部状态大小。
流密码的经验法则
• 如果您想要 k 位安全性,则内部状态大小必须至少为 2k 位。
• 在这种情况下,Babbage-Golic 攻击变得无效:
• 搜索空间 N = 22k
• T = M = D = P = 2k
• 另请注意,此攻击是通用的。
• 也就是说,攻击的适用独立于特定设计的内部结构。
在线/离线签名
目标再次相同:
使实时(在线)签名尽可能高效
• 回想一下,对于传统签名,我们使用散列和签名范式。
• 也就是说,我们首先对消息进行散列,然后对散列值进行签名。
• 如果我们也这样做,但添加一点“作弊”如何?
Trapdoor 陷门哈希函数
• 就像我们之前看到的散列函数一样,但有一个关键的区别 —— 散列函数有一个陷门Key。
• 没有陷门Key很难发现碰撞。
• 很容易发现与陷门Key的碰撞。
离散对数的陷门哈希
• 设 为一个安全的质数, 也就是说, 是个质数。
• 让$ g \in {2,3,…, 𝑝 − 1}$ 使得$ g^q = 1 \mod p$
• 选择一个随机 $ a \in {1,2,…, q−1 }$
• 设 $ y = g^a \mod p $
• $ H(m;r) = gmyr \mod p $ 用于一些消息 𝑚 和随机值 𝑟。
当给出:
假设是给定的且我们想要找到一个在的和的碰撞。
设
当未给出(见tut:基于不给定 α 的离散对数问题,证明 H 是抗碰撞的)
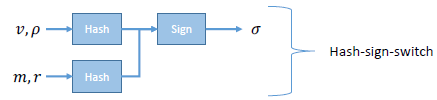
基于 Trapdoor 哈希函数的在线/离线签名
离线签名:
• 签署带有一些随机性𝜌 的随机消息𝑣。
在线签约:
• 收到实际消息𝑚
• 找到 𝑚 的taproot碰撞:即,设 $ r = a^{-1}(v-m)+ 𝜌$
在线/离线方案
考虑计算加密算法(加密、签名等)的设备功耗低的情况。
希望能够在消息到达之前预先计算一部分计算(即独立于消息!)。
• 可以进行预计算:要么提前通过另一个(更强大的)设备,并将结果嵌入到轻量级设备中;或当轻型设备连接到电源时
• 实时计算会更快,确保及时交付。
这种在线/离线设置主要用于非对称加密,因为它具有更繁重的运算,例如求幂和配对。
同样,我们有两个阶段:离线和在线。
• 离线阶段:在知道消息之前执行繁重的操作
• 在线阶段:使用给定的消息执行较轻的运算(乘法、加法等)
我们将重点关注两种特殊情况:
• Online/offline Identity-based Encryption (IBE) by Guo, Mu and Chen 基于 Boneh-Boyen IBE
• Shamir 和 Tauman 的在线/离线签名
Online/offline Identity-based Encryption
循环群
• 如果存在生成整个群𝐺的𝑔 ∈ 𝐺,则将群𝐺称为循环群
• 也就是说, 那么用 表示
• 例如,𝐺 = {1,2,…, 6} 是关于乘法的循环群,则存在
Diffie-Hellman 相关难题
设 G 是质数阶 p 的循环群,g 是 G 的生成器。
- 离散对数问题 (Discrete Logarithm Problem, DLP):如果 ,给定 h 和 g,很难得到 x
- 计算性 Computational Diffie-Hellman (CDH) 问题/假设:给定 和 ,很难计算
- 决策性Decisional Diffie-Hellman (DDH) 问题/假设:给定 , 和 ,很难判断是否
其中𝑥, 𝑦, 𝑎𝑛𝑑 𝑧 ∈ {1,…, p−1}
双线性配对 Bilinear pairings
令𝐺和𝐺是素数阶𝑝的循环群。 另外,让𝑔成为
𝐺的生成器。 那么,映射𝑒:,是一个双线性对,如果满足以下条件:
• 对于任何 𝑢,𝑣 ∈ 𝐺 和 。
• 。
• 映射 是有效地可计算的
Boneh-Boyen IBE
• Boneh-Boyen IBE 使用一次性签名方案,我们将用 和 表示(签名方案的公钥和私钥用𝑝𝑘 和𝑠𝑘 表示。
• 安全性基于Diffie-Hellman 问题的变体,称为Decisional Bilinear Diffie-Hellman 问题。
• 令 G 和 是 q 阶循环群,g 是 G 的生成器
• 让映射e: 是一个双线性对。
• 给定, 和,很难判断是否 ,其中h 是 中的随机元素, x, y 和 z ∈ {1, …, q-1}
设置
(红色部分为私密值
• 选择一个随机私密数
• 从G中随机选择, , , ,
• 设置
• 输出:公共参数 和主密钥
密钥生成
假设我们要为 生成一个私钥。
• 随机选择一个
• 计算
• 计算
• 输出:
加密
假设我们想要加密消息𝑚 ∈ 𝐺,对于某些身份𝐼𝐷 ∈ ℤ/。
• 选择一个随机
• 计算 和
• 计算 和
• 计算
• 输出:$ 𝐶 = (c_1, c_2, c_3, c_4, \sigma, pk)$
一个自然的在线/离线版本
• 我们可以预先计算所有不依赖于 𝑚 和 𝐼𝐷 的组件。
• 即预先计算:
• 剩余计算:
改进的在线/离线 Boneh-Boyen IBE
加密 - 离线阶段(消息m 和 ID 未知):
• 选择一个随机
• 计算 , 以及
• 计算 以及
• 计算
• 输出
加密 - 在线阶段(现在知道消息和 ID):
• 计算
• 计算
• 计算
• 输出:
对应的解密
• 检查是否
• 满足则计算
• 然后,我们就拥有与普通 Boneh-Boyen 加密相同的值
• 因此,其余的解密与原始 Boneh-Boyen 解密相同
在线/离线方案在计算效率方面最重要的优势是什么?答:在线阶段不求幂(exponentiation)!
Tut
文字题略
以下哪项可以代表权衡攻击的复杂性? 为什么?
(T = 时间复杂度,M = 内存复杂度,D = 数据复杂度)
只有 (3) 是不正确的,因为在这种情况下所有复杂性都随着 d 增加/减少。
假设A1是一个权衡攻击,离线时间复杂度为1天,在线时间复杂度为1分钟。 此外,让 A2 成为另一种权衡攻击,离线时间复杂度为 1 小时,在线时间复杂度为 1 小时。 计算两种攻击打破所需的时间
(a) 10 个密文,
(b) 120 个密文,
© 1200 个密文。
如果您是一个试图查看所有社交媒体用户之间交换的所有消息的恶意对手,您更喜欢哪种攻击?
(a) A1:以小时为单位的总时间 = 24 + 10 * 1/60 < 25。
A2:以小时为单位的总时间 = 1 + 10 * 1 = 11。
(b) A1:以小时为单位的总时间 = 24 + 120 * 1/60 = 26。
A2:以小时为单位的总时间 = 1 + 120 * 1 = 121。
© A1:以小时为单位的总时间 = 24 + 1200 * 1/60 = 44。
A2:以小时为单位的总时间 = 1 + 1200 * 1 = 1201。
在给定的场景中,攻击者希望破解大量密文。 因此,对于给定的场景,A1 将是首选,因为破解大量密文所需的总时间会少得多。
假设您要设计一个更新功能不使用密钥的密钥流生成器 (KSG),并且您需要 256 位的安全性。 以下哪项可能是可接受的内部状态大小?
由于流密码设计的经验法则(在状态更新函数中不使用密钥),内部状态大小必须至少是所需安全级别的两倍。 因此,内部状态大小必须至少为 512 位,并且只有 © 和 (d) 是可以接受的
让 Tiny 成为具有 64 位内部状态的轻量级流密码。 此外,假设 Tiny 在其状态更新函数中没有生成密钥。 给定一个密钥流序列,假设我们想要恢复正确的内部状态。
(a) 如果我们发起暴力攻击,所需的总时间、内存和数据是多少? 假设尝试一个候选内部状态需要 1 微秒。
(b) 如果我们发起时间/内存/数据 (TMD) 权衡攻击,所需的总时间、内存和数据是多少? 假设尝试一个候选内部状态需要 1 微秒
对于 (a),内存和数据的复杂性可以忽略不计(大约为 64 位)。
时间 Ta 将是
Ta = 264 · 10−6 秒 ≈ 244 秒 > 500.000 年。
另一方面,如果我们对 (b) 应用简单的 Babbage-Golic 权衡攻击,时间 Tb、内存 Mb 和数据 Db 复杂度将与整个搜索空间的平方根成正比 2 ^ {64/2} = 2^32。 更准确地说,我们将有
Tb = 2^32 · 10^{−6} 秒 ≈ 72 分钟
Mb = 2^32 · 2 · 64 位 = 236 字节 = 64 GB(存储了 2^32 个 64 位状态和 64 位密钥流块)
Db = 2^32 + 64 位 ≈ 2^29 字节 = 512 MB
请注意,通过在连续块中重叠 63 位,我们可以从 2^32 + 64 位的密钥流中得到 2^32 个 64 位的块。 另请注意,以预计算时间和内存复杂性为代价,可以降低数据复杂性(在攻击者无法访问大量数据的情况下)。
比较原始 Boneh-Boyen 基于身份的加密 (BB-IBE)、自然在线/离线 BB-IBE 和 改进的在线/离线 BB-IBE 的在线时间复杂度(在操作数量方面),如下所示。 确定哪一种最有效。

回想一下,“自然线上/线下”的第二步配对操作是在离线阶段完成的,在线阶段只有乘法。 另外,请注意,“改进的在线/离线”的 β-1 可以在离线阶段计算,而 c3 的计算是整数。 因此,可以非常有效地计算 c3,因此我们可以忽略
| Scheme | Pairing | Exponentiation | Signing | Group Multiplication |
|---|---|---|---|---|
| Original | 1 | 6 | 1 | 3 |
| Natural | 0 | 1 | 1 | 2 |
| Improved | 0 | 0 | 1 | 1 |
回忆一下讲座中介绍的基于离散对数问题的陷门哈希函数。 设 p, q 是 q = (p−1)/2 的素数,g ∈ G 的阶为 q(即 gq = 1)。 设置 y = gα 为一些随机 α ∈ {1, . . . , q − 1}。 定义散列函数 H(m; r) = gmyr。
(a) 基于不给定 α 的离散对数问题,证明 H 是抗碰撞的。
(b) 当给定 α 时,它是否抗碰撞?
(a) 假设已知 H(m1; r1) = H(m2; r2). Then
$g{m1}y{r1} = g{m2}y{r2}\g{m1}g{\alpha r1}=g{m2}g{\alpha r2} & \text{since } y = g^\alpha \ g^{m1+\alpha r1} =g^{m2+\alpha r2}\ m1+\alpha r1 = m2+ \alpha r2 \ \alpha(r1-r2)=m2-m1\ \alpha= (m2-m1)(r1-r2)^{-1} $
因此,只要发现碰撞使得 ,就可以很容易地找到 y 相对于 g 的离散对数 。 因此,如果我们假设离散对数问题很难,那么没有人应该能够轻松恢复,因此 H 必须是抗碰撞的。
(b) 否。当已知时,可以很容易地发现讲座中所示的碰撞。 例如,选取 并设 。 那么,H(m1;r1) = H(m2;r2)。
W10: DB Security - Searchable Encryption 可搜索加密
考点:可搜索加密,类别&查询类型,2个典型原型(Deterministic,Order preserving),泄露,泄露滥用攻击,更强安全保障是原型(CryptDB,FHE)
External adversary 外部对手
- 访问控制:用户名密码
- 防火墙:防止 DoS 攻击
- 软件补丁:防止 SQL 注入
Internal adversary
- 加密:最后的“门户”! (前提是密钥是安全的!)
可搜索加密
普通加密,例如 AES 和 RSA,不起作用(有效地):
- 没有可搜索性
- 需要解密密文
- 将敏感数据暴露给云服务器是不安全的
可搜索加密
- 允许从加密数据中搜索关键字
- 用户从关键字生成搜索标记
- 搜索请求的令牌发送到服务器,服务器返回一组包含此关键字的加密文档
- 服务器对关键字一无所知,只知道包含该关键字的加密文档的数量(理想情况下)
类别
支持的操作
- 静态 SE:仅搜索查询
- 动态 SE:插入、删除、更新和搜索查询
密钥管理
- 单用户
- 单个数据写入器和多个数据读取器
- 多个数据写入器和多个数据读取器
加密原语
- 对称 SE (SSE)
- 公钥 SE (PKSE)
威胁模型
- SE → 诚实但好奇的对手(半信任)
- 可验证的 SE → 恶意对手
查询类型
- 单关键字搜索,例如,keyword=“searchable encryption”
- 范围查询,例如 年龄 >18
- 布尔查询,例如“蒙纳士大学”和“学生”
- 排名搜索,例如 查找与“SE”最相关的文档
更复杂的查询,例如 count、max 和 group by,可能需要依赖
- 同态加密 (HE)
- 可信执行环境 (TEE)
Searchable Encryption Primitive
确定性加密 Deterministic Encryption (DE)
相同的输入(明文),相同的输出(密文):即没有随机性,例如 AES-ECB(相同的IV),
最简单的方案:客户端使用 DE 方案使用每列密钥 K 加密数据库的每一列
DE 保留明文的平等性并允许简单有效的搜索
许多行业兴趣和一些用途(例如 CryptDB
保序加密 Order Preserving Encryption (OPE)
DE 快速、简单且与现有 DBMS 兼容
但是,问题:如何搜索范围?如果使用普通 DE 则不可能
例如。 如果我们使用 AES 加密 (1,2,3),我们可能会得到:
— 8493540201039434290 = ENC(1)
— 2939025796054939211 = ENC(2)
— 1040304585702197218 = ENC(3)
每个密文看起来像一个随机数
明文顺序之间没有关系
一种特殊类型的 DE 称为保序加密 (OPE),即满足 如果 x < y 那么 Enc( x ) < Enc y
希望查询范围 [ a, b ] 的客户端改为向服务器发送范围 [ Enc(a), Enc(b)] 的查询
例如。
— 142321645 = ENC(1)
— 232402329 = ENC(2)
— 520403567 = ENC(3)
— 593029476 = ENC(4)
— 934820471 = ENC(5)
安全问题
DE 保留密文空间中明文的频率
假设攻击者有辅助信息——对明文分布的合理准确的估计。
CryptDB 正面临这个问题!
对服务器的泄漏对于 OPE 来说会更大
服务器不仅知道频率,而且知道明文的顺序!
例如。
– 第 1 列:学生证
– 第 2 栏:考试成绩
尽管服务器不知道任何标记的确切学生 ID,但服务器可能知道:
– 标记分布
– 学生的表现如何
CryptDB
第一个功能齐全的加密数据库系统, 由麻省理工学院的一组研究人员于 2011 年设计
Raluca Ada Popa , Catherine M. S. Redfield, Nickolai Zeldovich , and Hari Balakrishnan , CryptDB : Processing Queries on an Encrypted Database , In Proceedings of the 23rd ACM Symposium on Operating Systems Principles (SOSP ), 2011
代码:https://github.com/CryptDB/cryptdb
数据库中的机密数据泄露
威胁 1:被动(内部的)数据库服务器攻击
威胁 2:对所有服务器的任何攻击(外部)
目标:保护数据的机密性
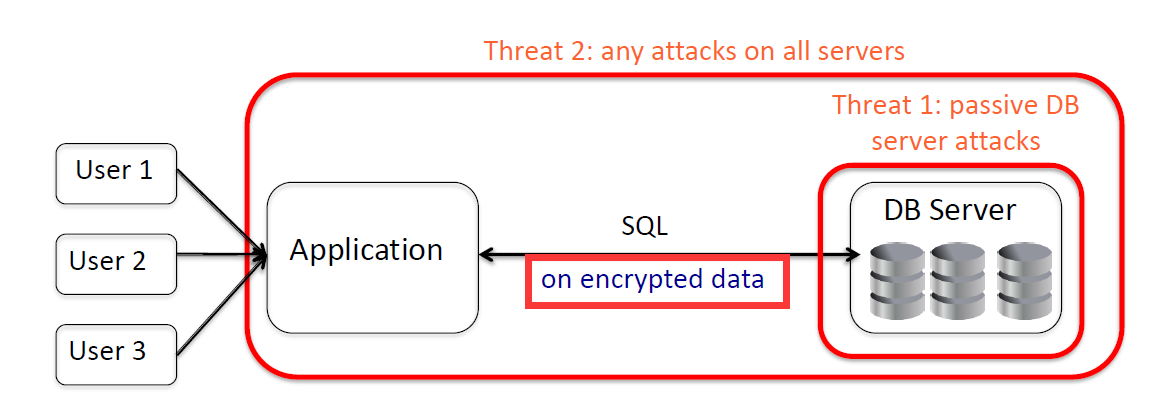
- 处理对加密数据的SQL查询
- 使用细粒度的键(fine grained keys); 根据访问控制将这些密钥链接到用户密码
贡献:
- 第一个实用的 DBMS 来处理对加密数据的大多数 SQL 查询 → Hide DB from sys. admins ., 将数据库外包到云端
- 保护在攻击期间注销的用户数据,即使所有服务器都受到威胁
- 适度的开销:TPC C 26% 的吞吐量损失
- DBMS(例如 Postgres、MySQL)没有变化,对于威胁 1,应用没有变化
Threat 1: Passive attacks to DB Server
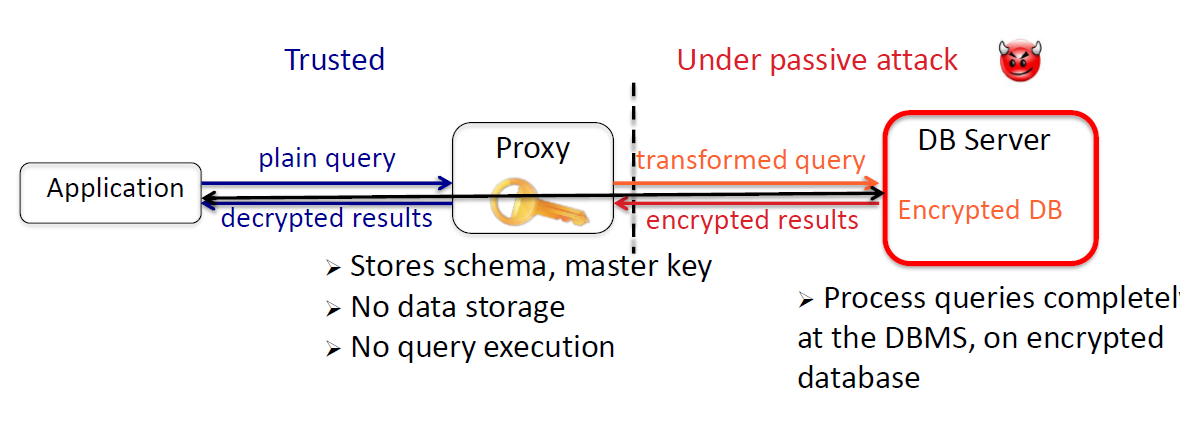
处理对加密数据的 SQL 查询 (本质就是用上面的OPE处理值
两种技术
- 使用 SQL 感知加密方案集
- 根据查询调整数据库加密
加密模式
列名: 模式 | 构造器 | 功能
功能性Functionality与安全性反向
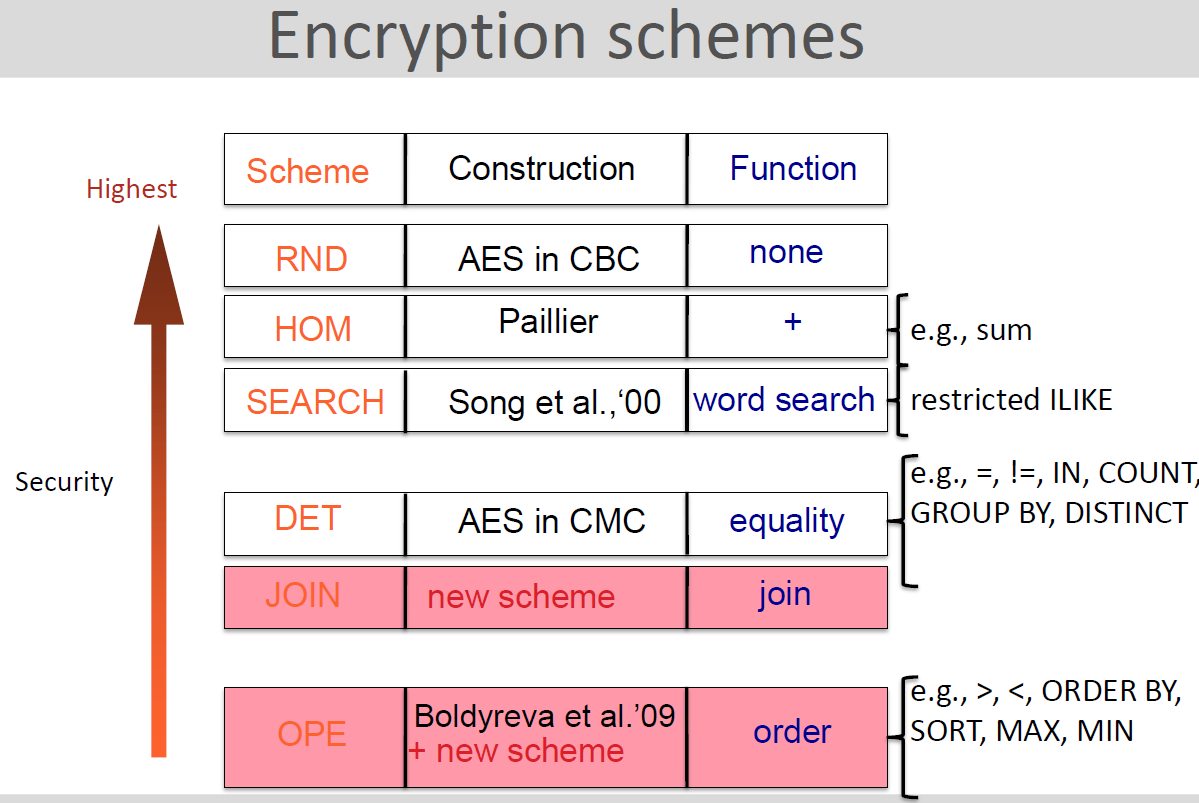
JOIN
攻击者不知道列要加入先验(就是图中的key for col)!
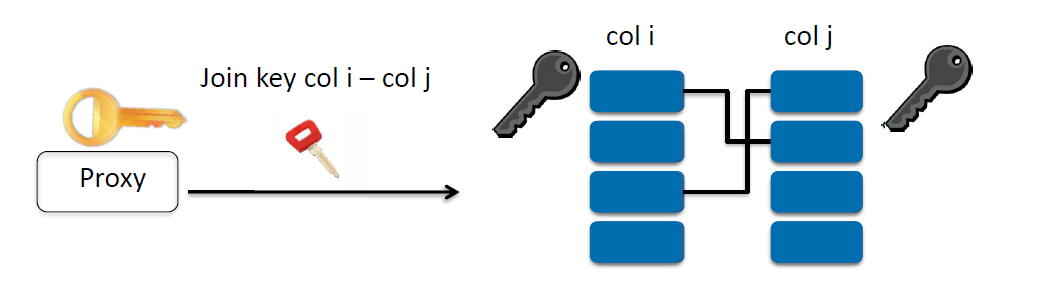
- KeyGen (sec. param ): SK (最左边黄Key)
- Encrypt (SK, m, col i ): (使用私钥(不在图中)) → deterministic
- Token (SK, col i , col j): , (使用左二红Key)
- Adjust( , ): (使用最右灰Key)
正确性:调整产生正确的Join关系
安全性:无法得知没有令牌的连接关系
实现:192 位长,0.52 毫秒加密,0.56 毫秒调整
如何加密每个数据项?需要的加密方案取决于查询,提前可能不知道查询, 如图在使用rank时候在OPE阶段泄露了值的顺序
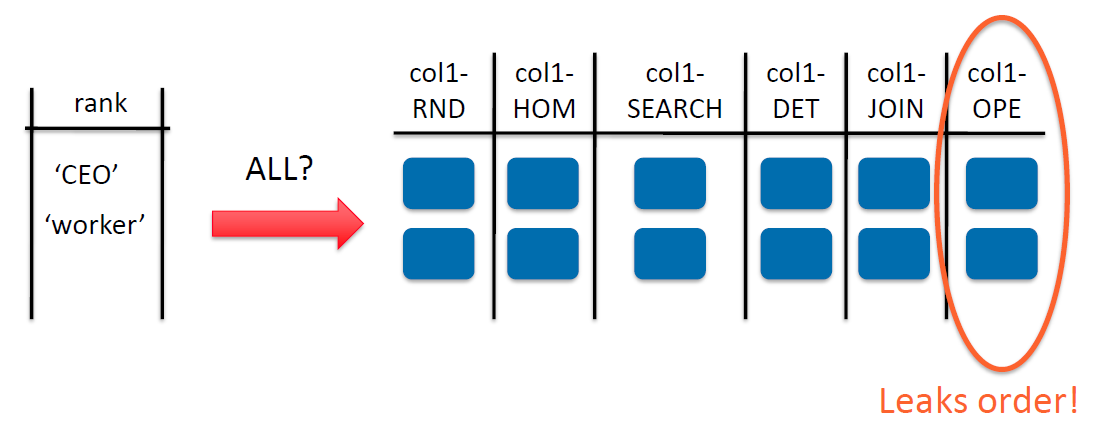
因此需要加密“洋葱”模式Onions of encryptions,通过包裹加密来保证安全
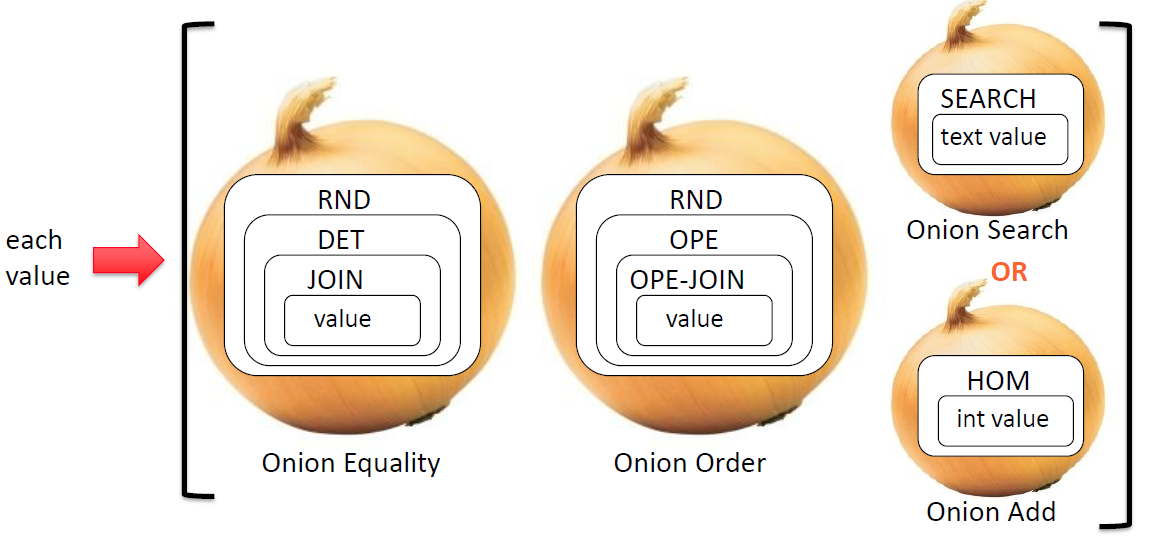
同一洋葱层的列中所有项目使用相同的Key
以最安全的加密方案启动数据库
例如:SELECT * FROM emp WHERE rank = 'CEO'修改为
1 | UPDATE table1 SET col1 OnionEq Decrypt_RND(key, col1 OnionEq); // 使用新table存放RND值 |
DB Implementation
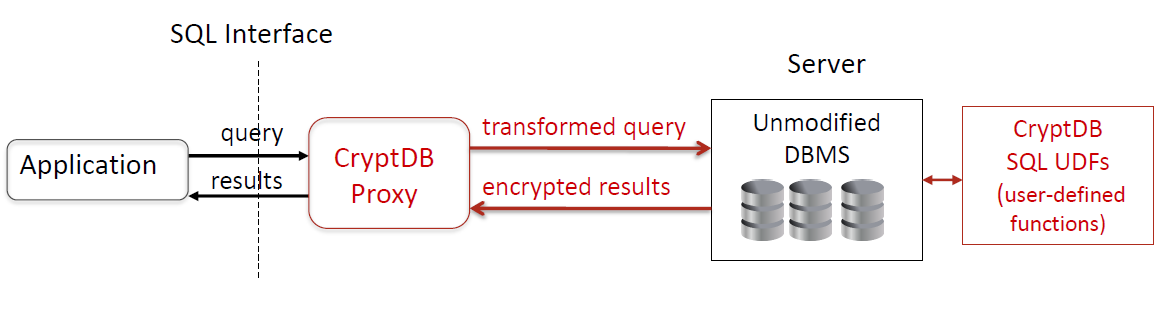
DBMS 层 没有变化
便携:从 Postgres 到 MySQL 86 行
威胁 1 解决方案: 无需更改应用程序
性能损失26%
Searchable Encryption中的泄漏
如果我们使用概率加密来加密记录和查询会怎样? 可以隐藏频率和订单信息
访问模式泄漏:
• 有多少记录匹配每个查询(大小模式泄漏
• 哪些记录与每个查询匹配
• 查询是否匹配相同的记录
Leakage-abused Attacks 泄漏滥用攻击
被动攻击
- IKK (访问模式
- 计数攻击Count attack(大小模式
- 频率分析攻击Frequency Analysis Attack(频率信息。
- 。。。
主动攻击
- 文件注入攻击 (访问模式
- 选择文档攻击(访问模式
- 记录注入攻击(访问模式
- 。。。
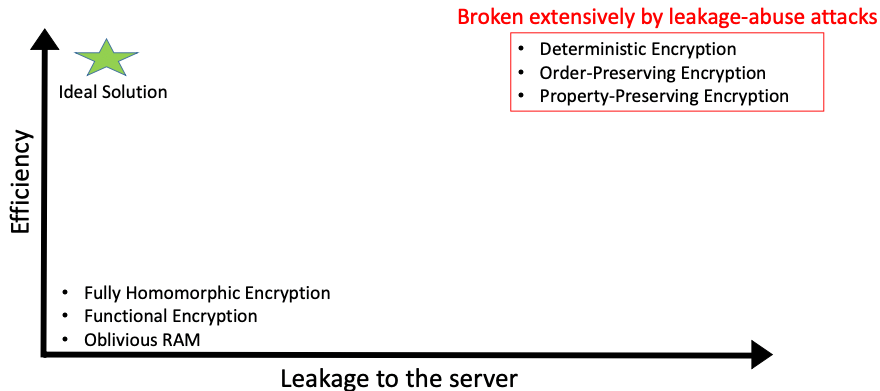
可搜索加密的权衡
理想位置如图五角星处,右上是被泄漏滥用攻击广泛破坏的,左下是完全同态加密,功能性加密,遗忘内存
同态性质
其中 • 是明文域中的一些操作, 是密文域中的一些操作
• 有助于获得隐私保护财产
• 对加密数据的计算
• 节省隐私保护网络应用程序的通信成本
例如RSA的同态性 RSA is homomorphic
使 其中 x 表示乘法,在RSA的加密
则可得$E(p_0)\times E(p_1) = p_0^{pk}\mod n \times p_1^{pk}\mod n= (p_0\times p_1)^{pk} \mod n = E(p_0 \times p_1) $
Tut
文字题略
W11: Implementing and Protecting Cryptographic primitives 实施和保护加密原型
算法、攻击和对策
review里只有三类attacks(Non-, Semi-, invasive)
费马小定理寻找乘法逆
设 p 为质数,元素 a < p;
然后 否则
我们可以找到 a 的倒数(假设是 x,这样 )
⇒ ⇒ $ a−1 = a^{p-2} \mod p$ (在上)
例如
3 mod 5 的乘法逆
即$ 3^{-1} \mod 5 = 3^{5-2 } \mod 5$
验证:
(为了使定理有效,组中的所有元素必须有一个乘法逆,即。 Gcd(a,p)=1)
使用扩展欧几里得算法查找乘法逆
为了解决欧几里德算法非常数轮问题,我们使用扩展的欧几里德算法来计算 gcd(a,p) 使用以下公式:
然而,如果 gcd(a, p)=1,如 Ζp 的情况,则:
因此我们可以找到 的乘法逆
Euclid (a, p)
1 (X1,X2,X3) ← (1, 0, p); (Y1, Y2, Y3) ← (0, 1, a)
2 IF Y3 = 0, RETURN X3 = GCD (a, p); No inverse
3 If Y3 = 1, RETURN Y3 = GCD (a, p); Y2 = a-1 mod f
4 Q = X3/Y3
5 (T1,T2,T3) ← (X1 - QY1, X2 - QY2, X3 - QY3)
6 (X1,X2,X3) ← (Y1,Y2,Y3)
7 (Y1,Y2,Y3) ← (T1,T2,T3)
8 GOTO 2
在计算过程中,必须始终为True:
fT1 + dT2 = T3; fX1 + dX2 = X3; fY1 + dY2 = Y3
有限域(回顾)
有限元素个数 GF(p) = {0, 1, …, p-1}。
p:称为有限域字符 GF p 特征的素数
扩展有限域
当 q = p k 时,GF q 在 GF p 上
• k = 1: 质数场,GF(p)
• p = 2: 二元扩展有限域,
如何实现模运算?
GF(p) 字段(加减): 在 GF(p) 中定义为模加减法。
$(a+b) \mod p = \begin{cases} a+b & \text{if }a+b<p\ a+b-p & \text{if } a+b \ge p\end{cases} $
整数加法或减法
对于硬件:加减的相关架构是:Ripple Carry, Carry Lookahead, Carry Save, Carry Select ή Carry Skip adders
GF(p) 场(模乘)
步骤 1. 整数乘法(Karatsuba - Ofman
步骤 2. 对步骤 1 的整数乘法结果进行模 p 运算(Barret’s Reduction,Montgomery Reduction)
或者直接 整数乘法与模 p 约简
Montgomery 蒙哥马利算法:𝑐 = 𝑥 ⋅ 𝑦 ⋅ 𝑟^−1 mod 𝑝
Μodulo squareing : 模乘法适当简化,因为对于 𝒄 = 𝒙 ⋅ 𝒚 𝐦𝐨𝐝 𝒑 有 x = y。
蒙哥马利模乘法(MontM(x,y,p) 函数)
输入:$ x = {x_{n-1},…,x_2, x_1, x_0 }b < p,\ y = {y{n-1},…,y_2, y_1 , y_0 }b < p,\ p = {p{n-1},…, p_1, p_0 }_b,\ r = b^n, p^\prime = -p^{-1} \mod b$ b: 一个常数(通常是 2 的幂)
输出:
- c = 0
- 对于 i=0 到 n-1 做
2.1.
2.2. - 如果 那么 c = c – p
- 返回 c.
蒙哥马利域
有一个数字 ,而不是数字 X
在蒙哥马利域中的数字之间执行蒙哥马利乘法产生也在蒙哥马利域中的结果
模幂算法 Modular Exponentiation Algorithm
输入:g in G and x>0 ; 输出: G 中的
表示
1 | y ⟵ g, z ⟵ 1 |
例如
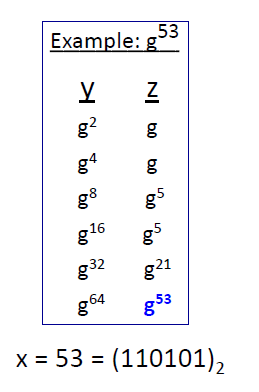
高效的模幂算法
蒙哥马利模幂(MontMexp(x,e,p) 函数)
输入:$ x = {x_{n-1},…,x_2, x_1, x_0 }2 < p,\ y = {y{n-1},…,y_2, y_1 , y_0 }2 < p,\ p = {p{n-1},…, p_1, p_0 }_2,\ r = b^n $ (通常 b=2 或 2 的幂)
输出:
- $ c= r\mod p $
- $g = r^2 \mod p $
- $\bar{x} = x \cdot g \cdot r^{-1} \mod p $
- For i in (n-1) to 0:
- $c = c \cdot c \cdot r^{-1} \mod p $
- if then
- $ c =c \cdot 1 \cdot r^{-1} \mod p$
- Return c
转换为蒙哥马利格式:
如果 G 中的 x(例如 GF(p) ή Ζp*)然后我通过在 a 和 r^2 mod p 之间执行蒙哥马利乘法来归一化 𝑥 ⋅ 𝑟 𝑚𝑜𝑑 𝑝(蒙哥马利格式)中的 x。 为什么?
如何从蒙哥马利格式转换为常规 G 元素?
基于离散对数问题的密码系统怎么样?
离散对数计算实际上是模幂运算蒙哥马利模幂运算算法也适用于此。
攻击模型
安全设备存储和处理机密信息。
主要的秘密是私钥或公钥
密码学是安全应用程序(硬件或软件)中的关键点
目标:
查找使用的密钥
通过检索会话密钥来利用安全协议
Non-invasive attacks (low-cost) 非侵入式攻击(低成本)
• 观察或操作设备,无需物理修改
• 不留下篡改证据——难以发现
• 只需要中等复杂的设备和知识即可实施
• 示例:功率分析攻击power analysis attacks、时序攻击 timing attack
Invasive attacks (expensive) 侵入性攻击(昂贵)
• 几乎无限的能力从芯片中提取信息并了解其功能
• 需要直接访问设备的内部组件
• 通常需要昂贵的设备、知识渊博的攻击者和时间
• 示例:微测 microprobing
Semi-invasive attacks (affordable) 半侵入式攻击(经济实惠)
• 我们可以在计算过程中注入故障并观察故障结果。 系统内部结构保持完整
• 填补了非侵入性和侵入性类型之间的空白,既便宜又易于重复
抗侵入性攻击(防篡改antitampering)
• 将整个安全核心包裹在细粒度的电子网格中
• 将核心包裹在环氧树脂中
• 光敏二极管、温度传感器、篡改传感器
• 检测电压和电流变化的传感器
• 当检测到攻击时,芯片应用数据归零,或者芯片变得无用
防篡改级别:
• 零级
• 级别低
• 关卡模型
• 关卡模组
• 级别模式
• 级别高
非侵入性(侧信道)攻击 SCA
安全模型:黑盒
攻击数学算法
控制输入/输出
但是:内部计算和密钥完全隐藏
现实:
攻击整个实现
实现泄漏了有关内部的部分信息
泄漏:例如功耗、运行时间、电磁辐射
side-channel 侧信道
• 针对不同计算时间的定时攻击
– 不正确的密码验证:在不正确的字节上终止,不同的计算
不正确字节的长度
– 加密算法的错误实现:性能优化、缓存
内存使用,非固定时间操作
• 今天:传统的计时攻击变得更难应用
– 制造商修复了常见错误
– 内部时钟源和 PLL 的使用使分析变得困难
– 对策已到位:随机时钟、虚拟周期
– 仔细选择硬件可消除许多问题
但…。 由于处理器使用缓存内存导致的时序泄漏!!
功耗分析 Power analysis:及时测量功耗
– 非常简单的一套设备 – 一台带有示波器和电源线中的小电阻的 PC;对许多密码算法和密码验证方案非常有效
– 需要电气工程和数字信号处理方面的一些知识
– 两种基本方法:简单(SPA)和差分(DPA)
电磁分析 Electro-magnetic analysis (EMA):测量发射
– 类似于功率分析,但不是电阻器,而是使用小型磁性线圈,允许在芯片上进行精确定位
今天:SPA/DPA 和 EMA 变得更具挑战性
– 更高的工作频率和噪音:需要更快的设备
– 电源从 5V 降至 1V:信号更低,噪声更大
– 8 位数据与 32 位数据:更难区分单位变化
– 更复杂的电路:来自其他部件的噪声更高,因此需要更多的信号平均和数字信号处理
– 许多密码算法的有效对策
攻击类型
简易攻击
攻击者直接使用来自一次测量的旁道信息来确定(部分)密钥。 简单的分析攻击利用了执行的操作和侧信道信息之间的关系。
差分攻击
• 使用许多测量来滤除噪声。 差分分析攻击利用了处理过的数据和侧信道信息之间的关系。
• 被攻击设备的假设模型:该模型用于预测
• 设备边信道信息的几个值。
• 将这些预测与实际测量的设备侧信道信息进行比较。 通过对数据应用统计方法进行比较。
时序攻击
基本思想:通过观察执行各种计算需要多长时间来了解系统的秘密
典型目标:提取私钥
非常强大,因为隔离无济于事
• 受害者可能是远程的
• 受害者可能在自己的虚拟机中
• 钥匙可以放在防篡改存储或智能卡中
攻击者只需测量响应时间即可获胜
缓存攻击
• 缓存攻击:通过缓存地址泄漏进行密码分析
• 纯软件
• 无特殊特权
• 不与加密代码交互
• 非常高效
• 在 65 毫秒内从 Linux 加密分区中提取完整的 AES 密钥
• 损害其他安全性良好的系统
• “商品化”侧信道攻击:
• 易于部署的软件会破坏许多常见系统
Address leakage 地址泄露
• 缓存是共享资源:
• 缓存大小有限:L1 缓存限制在 8 KB 到 64 KB 之间
• 进程/线程争夺缓存
• 缓存状态影响并受所有进程/线程的影响,导致进程/线程之间的串扰
• 缓存数据受内存保护……
• 未受攻击
• 但是“元数据”会泄露有关内存访问模式的信息:正在访问哪些地址。
差分侧信道攻击
• DPA (differential power analysis)统计原理
– 收购程序
– 选择和预测
– 微分运算符和曲线
– 使用 DPA 指标进行逆向工程
案例:微分功耗攻击的步骤
- 在设备上随机消息的正常加密/解密过程中收集电源跟踪
- 对Key进行假设,并基于该假设密钥上的已知功率模型收集功率轨迹
- 对各种关键位重复假设
4.对未知正确密钥的假设密钥功率迹线和实测功率迹线之间进行统计分析(例如相关性)。 - 提取加密/解密密钥。
案例:使用垂直(相关分析)攻击攻击 AES 硬件易受攻击的实现
功耗模型
● 功耗如何取决于中间值
● 单位模型——例如。 最低位(v)
● Hamming weight: HW(v)
○ 主要适用于处理器、带上拉的总线等。
● Hamming distance:
○ 也适用于 ASIC、FPGA
○ v’ 是前一个值(在寄存器中,在总线上,在门中)
○ 如果 v’ 是常数或不均匀分布,通常 HW 也能工作
计算相关性Correlation
● 存在多种方法
○ 均值差、均值距离、相关系数
● 相关系数
● 更精确的点估计
● 范围
半侵入式攻击(故障注入)
紧急故障Glitch Faults
• 时钟
• 电压
• 数据损坏
激光束、聚焦离子束等
目标:
• 随机字节或位翻转
• 字节中的特定位
• 在选定的时间内随机或特定位或字节翻转
故障注入安全错误
蒙哥马利功耗梯故障注入安全错误
对策
SCA侧信道攻击对策
• 算法变异对策
– 掩蔽/致盲 → 随机化可与敏感信息相关联的数据
– 提供最终消除盲区的方法(在算法内)。
• 基于实施的对策
– 隐藏:使泄漏跟踪独立于中间值和执行的操作。
– 使泄漏迹线无法与噪声区分开来
– 使泄漏跟踪恒定(例如双轨逻辑、预充电逻辑、互补电路)
故障注入攻击对策
• 故障检测机制
– 面向实现(类似于防篡改)
– 面向算法(观察中间值数学或二进制值的一致性)
– 时间冗余
– 硬件冗余
– 信息冗余
• 确保故障始终传播
– 不要使用虚拟操作(与秘密数据相关)
– 感染计算原理:用一些隐藏数据感染计算,使故障注入无用
– 随机化
Tut
基本上是内容回顾了
Using Fermat’s theorem, find 3^2001 mod 11
Fermat’s Theorem states
if p is prime and a is a positive integer not divisible by p, then a^{p−1} mod p ≡ 1. Therefore 3^10 mod 11 ≡ 1.
Therefore 3^2001 = (3^10)^200 × 3 mod 11 = 1 × 3 mod 11 = 3
Using Multiplicative inverses Fermat little Theorem, find the multiplicative inverse of 3 mod 5?
The multiplicative inverse of 3 mod 5 is 3^{-1} mod 5 = 3^{5-2} mod 5
Therefore 3^3 mod 5 = 27 mod 5 = 2
Using Multiplicative inverses Fermat little Theorem, find the multiplicative inverse of 8 mod 17?
8^{-1} mod 17
8^{17-2} mod 17 = 8^15 mod 17 = 8^7 * 8^8 mod 17 = 15 * 1 mod 17 = 15
文字题略
W12: Blockchain
密码学集大成者
似乎不在考试范围中!(至少review里没
因为太懂了所以略
Exam
• 20道选择题(共10分,每道0.5分)
• 6-8 道小作文题(共 50 分)
• 2 小时 + 10 分钟
哪种密码块操作模式(ECB 或 CBC)更常用? 给出使用 CBC 优于 ECB 的一项优势和使用 CBC 优于 ECB 的一项劣势。
回想一下,对称密钥密码系统由三个函数组成:密钥生成器 G、加密函数 E 和解密函数 D。对于任意一对用户,例如 Alice (A) 和 Bob (B),G 将 a 作为输入 随机位串并产生共享密钥 KAB 作为输出。 Alice 或 Bob 都可以获取明文消息 x 并产生密文消息 y ← E(x, KAB)。 密文 y 可以通过不安全的通道发送,接收者可以恢复 x ← D(y, KAB)。
a) 简要说明此类系统安全的三个基本要求。(可能是安全服务3目标,也可能是MAC部分提到的三原型
b) 为什么对称密钥密码学不足以作为安全互联网通信的基础,尤其是安全的基于 Web 的商务?(W5&W6开头有写对称的缺点
Mock里最后一题有点难,估计会出类似题目(换公式

这里(第9页)有个类似的答案
可能文不对题但是思路应该是一样的(Protocol A一致B不一致,答案对应的是
(a) 提供接收者在收到 y 时所做的事情的逐步描述:
解决方案:
接收方执行以下操作,协议 A:
• 使用k1 解密并获得x||H(k2||x)。 提取 x。
• 散列k2||x 并与H(k2||x) 进行比较。
对于协议 B(完全有缺陷):
• 使用k_priv 解密并获得H(x)。 提取 x。
• 散列 x 并与 H(x) 进行比较
(b) 说明是否有以下安全服务:
• 保密
• 正直
• 不可否认性
为前一问题中给出的两个协议中的每一个给出。
解决方案:
在协议 A 的情况下:
• 保密性 - 是通过加密
• 完整性 - 是通过散列
• 不可否认性——双方都不能声称对方已经创建了消息。
在协议 B 的情况下:
• 机密性 - 不,没有加密
• 完整性 - 不,因为任何人都可以替换消息并计算散列
• 不可否认性- 没有人可以创建这样的消息。
(原题答案应该B是三性都有的,本质就是类似 AES_共有密钥(原文+签名)