Notes for FIT9136: algo & python

发表于 更新于

相对简单

W5

OOP

py3直接用class XXX:而不是2的class XXX(object): (3里俩写法等价)

W6

Stack: LIFO

Queue: FIFO

Heap: 就是一种特殊的树Tree。顶部（root）为一个极值（子树也是）。其中Node之间的连接叫Edge

W7

Complexity

复杂度这个概念和后面的各个算法都有关，所以挺重要的。

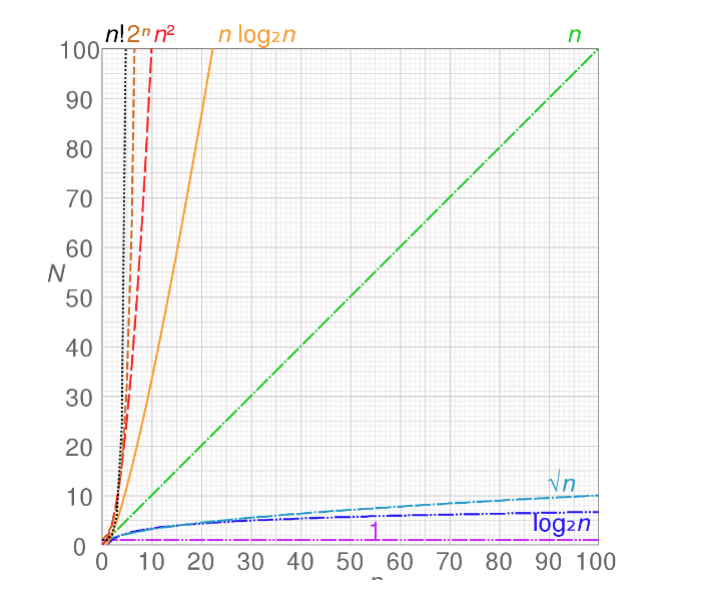
计算方法是：

把算法函数内每个步骤的复杂度取出来，然后+起来

比如

2N + 2 -> O(n)

n^2 + n + 1 -> O(n^2)

log(n) + n + a -> O(n)

本质就是留下复杂度最大的那个（瓶颈）

这里1，N，N^2，N^N这些复杂度都很好理解。

但是log(N)是什么情况？

stackoverflow这里给的例子就比较全面。

O(log n): 选择要在其上执行某些动作的下一个元素是几种可能性之一，并且仅需要选择一个。

例如：给定一个人的名字，找到他的电话号码。所用方法是在尚未搜索的那本书（有序！）的一半左右随机选择一个点，然后检查该人的名字是否在该点上。 然后在此人名字所在的部分的一半左右重复该过程。（即对人名的binary search，二分法）

O(n log n): 打印机办公室里有些混乱，我们的电话簿中的所有页面都是随机插入的。 通过查看每个页面上的名字，然后将该页面放在新的空电话簿中的适当位置，可以更正顺序，使其正确无误。

Searching Algorithm

Linear Search太简单，就一个个代，略

Binary Search参考上面O(log n)解析

Sorting Algorithm

Bubble Sort: 就左右互换直到所有 左<右。一般就先把最大/最小挪到位然后再排。平均和最坏都是O(n^2)，最好是O(n)

1
2
3
4
5
6
7
8
9
10
11
def bubble_sort(the_list):
    n = len(the_list)
    
    for i in range(n-1, 0, -1): 
        for j in range(i): #上个for从maxIndex到0,就是为了在这里省的写[0,index]直接range表示了
            if the_list[j] > the_list[j+1]:
                temp = the_list[j]
                the_list[j] = the_list[j+1]
                the_list[j+1] = temp
                
    return the_list

Selection Sort: 找index后面最小的然后互换。O(𝑛^2)

1
2
3
4
5
6
7
8
9
10
11
12
def selection_sort(the_list):
    n = len(the_list)
    
    for i in range(n-1):
        smallest = i
        for j in range(i+1, n):
            if the_list[j] < the_list[smallest]:
                smallest = j

        the_list[smallest], the_list[i] = the_list[i], the_list[smallest] #交换
    
    return the_list

Insertion Sort: 把每个源数组的元素有序地丢到新数组里。（比如先丢5，然后看见8了再丢5后面，看见7了确定丢5和8中间）。O(𝑛^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
def insertion_sort(the_list):
    n = len(the_list)

    for i in range(1, n):
        current = the_list[i]
        pos = i
        while pos > 0 and the_list[pos-1] > current:
            the_list[pos] = the_list[pos-1]
            pos -= 1

        the_list[pos] = current #丢
        
    return the_list

W8

二叉树和二叉搜索树

二叉树本身不带规则，只规定这形状，要用起来就得自己给它加点规则

二叉搜索树就是带了“左边小于右边”这个规则

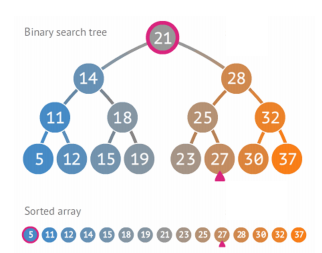
Breadth（宽度） First Search (BFS)，即优先找横的（跨node！）

Depth First Search (DFS)，即优先找竖的（顺藤摸瓜）

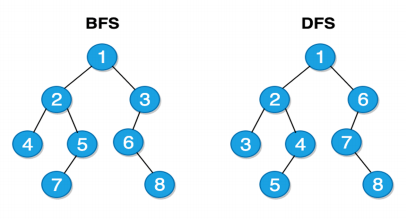
这些1234是查找时候的序列，不是值

另外还有个平衡Balance的概念，就把深度对对齐（±1）。

Balance有助于减少搜索步数N -> logN

W9

测试，错误处理和外部库（讲的标准库，numpy，pandas和matplotlib）

assert onFalse, “err”

对于代码

1
2
3
4
5
6
7
mark = 0 # variable to change
if mark >= 50 and mark <= 100:
    grade = "Passed"
else:
    grade = "Failed"
    
print(grade)

  • Valid (positive) cases:

    • Based upon “correct” input data
    • Examples: 55, 60, 65, …, 85, 90, 95, …

  • Invalid (negative) cases:

    • Based upon “incorrect” input data
    • Examples: -1, 0, 5, …, 45, 49, 101, 200, …

  • Boundary cases:

    • Boundary values of the “equivalence class” for valid cases
    • Examples: (49, 50) and (100, 101)
    • 即一个pair，其中元素一个能success一个就fail

W10

文件，库和包（RegExp）

W11

11和12有点难，Quiz11-12直接大意失荆州。

Divide-and-Conquer

大意就是将func中任务细分（divide）然后逐个解决（conquer）最后合并（combine）

Binary Search是作为Divide-and-Conquer的例子出现的，并不是之前的BST（Binary Search Tree，w8内容）

迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def binary_search(the_list, target_item):
    low = 0
    high = len(the_list)-1

    while low <= high:
        mid = (low + high) // 2

        if the_list[mid] == target_item:
            return True
        elif target_item < the_list[mid]:
            high = mid - 1
        else:
            low = mid + 1

    return False

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def rec_binary_search(the_list, target_item):
    if len(the_list) == 0:
        return False
    else:
        mid = len(the_list) // 2

        if the_list[mid] == target_item:
            return True
        elif target_item < the_list[mid]:
            smaller_list = the_list[:mid]
            return rec_binary_search(smaller_list, target_item)
        else:
            larger_list = the_list[mid+1:]
            return rec_binary_search(larger_list, target_item)

Recursive

递归，简单，略

Merge Sort

Merge Sort是作为Recursive的例子出现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
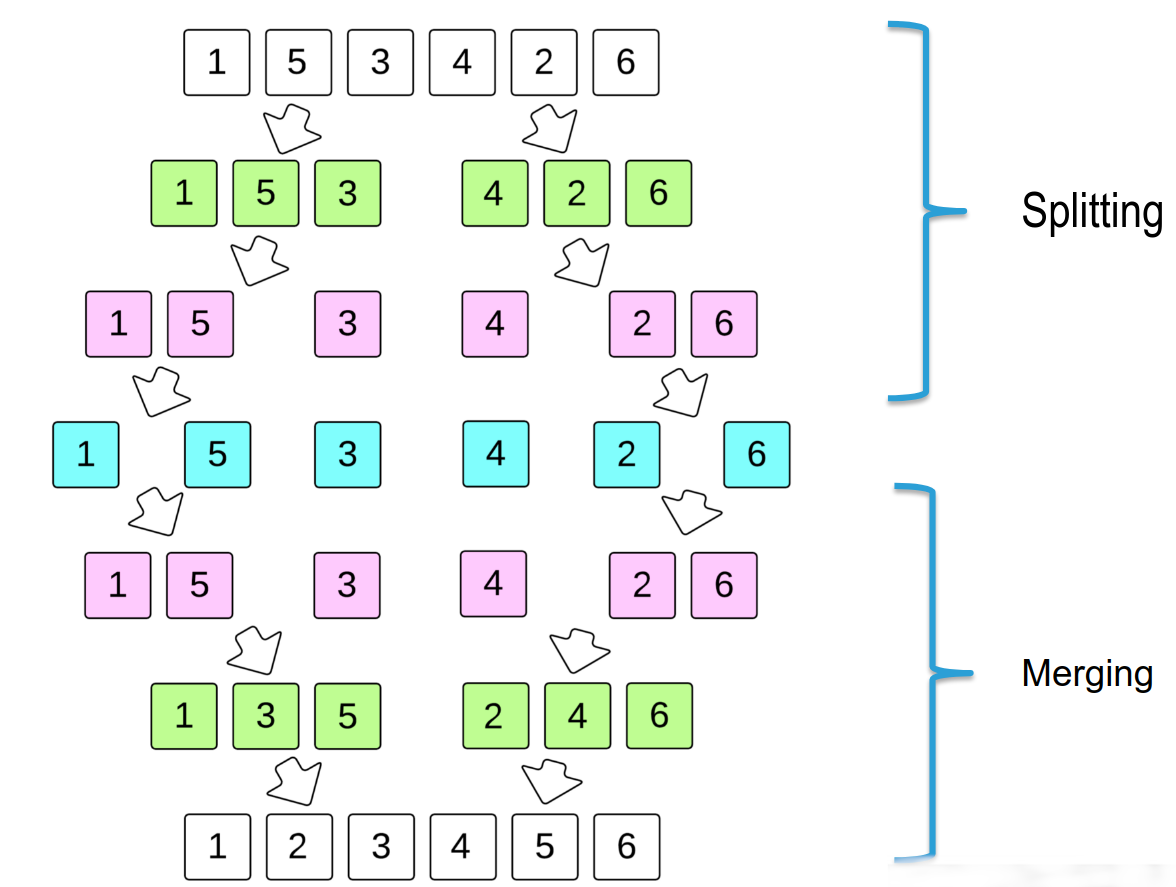
34
def merge_sort(the_list):
    n = len(the_list)
    
    if n > 1:
        mid = n //2 

        left_sublist = the_list[:mid]
        right_sublist = the_list[mid:]

        merge_sort(left_sublist)
        merge_sort(right_sublist)

        i = 0 # index for left sublist
        j = 0 # index for right sublist
        k = 0 # index for main list
        
        while i < len(left_sublist) and j <len(right_sublist):
            if left_sublist[i] <= right_sublist[j]:
                the_list[k] = left_sublist[i]
                i += 1
            else:
                the_list[k] = right_sublist[j]
                j += 1
            k += 1

        while i < len(left_sublist):
            the_list[k] = left_sublist[i]
            i += 1
            k += 1
            
        while j < len(right_sublist):
            the_list[k] = right_sublist[j]
            j += 1
            k += 1

Quick Sort

Quick Sort也是作为Recursive的例子出现。

  • Divide: Select a “pivot” to serve as the partition point
    • Elements smaller than the pivot are relocated to the left of the pivot
    • Elements greater than the pivot are relocated to the right
  • Conquer: Recursively partition the sublists based on the pivot chosen for each sublist
  • Combine: No computation needed
  • Base case: A sublist with length of one (considered sorted) or with zero length
  • Best case: O(n*log(n)) Worst case: O(n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def quick_sort(the_list):
    first = 0
    last = len(the_list)-1
    quick_sort_aux(the_list, first, last)
    
def quick_sort_aux(the_list, first, last):
    if first < last:
        part_point = partitioning(the_list, first, last)

        quick_sort_aux(the_list, first, part_point-1)
        quick_sort_aux(the_list, part_point+1, last)
        
def partitioning(the_list, first, last):
    pivot_value = the_list[first]

    left_index = first + 1
    right_index = last
    
    complete = False
    
    while not complete:
        while left_index <= right_index and \
            the_list[left_index] <= pivot_value:
                left_index += 1

        while right_index >=  left_index and \
            the_list[right_index] >= pivot_value:
                right_index -= 1

        if right_index < left_index:
            complete = True
        else:
            the_list[left_index], the_list[right_index] \
            = the_list[right_index], the_list[left_index]
                
    the_list[first], the_list[right_index] \
                = the_list[right_index], the_list[first]
        
    return right_index

W12

Greedy Algorithm

  • 适合通常不会产生最佳解决方案的情况（就是没法直接一个solution直接撸
  • 解决背包问题（Knapsack，即怎么把东西放到容量有限的背包里能收益最大化）
  • greedy不会先想着去满足最优，而是先想着把要求（塞满背包）给优先满足
  • 有时，任何一种立马得出的解决方案都比几天之内才想出来的的最佳解决方案要好。
  • 通常，某些算法会在运行时找到最佳解决方案，但需要一种假设的解决方案才能开始工作。 Greedy可以很容易地做到这一点。

Brute-Force

  • 保证算出最优解Brute force guarantees the optimal result will be discovered because it explores every possibility.
1
2
3
4
5
6
7
8
9
10
11
def brute_force(solution, N):
    if len(solution) == N:
        print(solution)
    else:
        options = getOptions()

        for option in options:
            brute_force(solution + option, N)

def getOptions():
    return [ str(i) for i in range(0,10) ]

Backtracking

  • Backtracking is an improvement on Brute-force. It ensures that only solutions that are possible are generated.
  • Backtracking is a more elegant brute force. Behold(看作) what happens when brute force attempts to find a solution.

用来解决类似N皇后（N*N的棋盘上放N个皇后）问题。本质也是暴力穷举

错题

What is the name of the following sort algorithm?

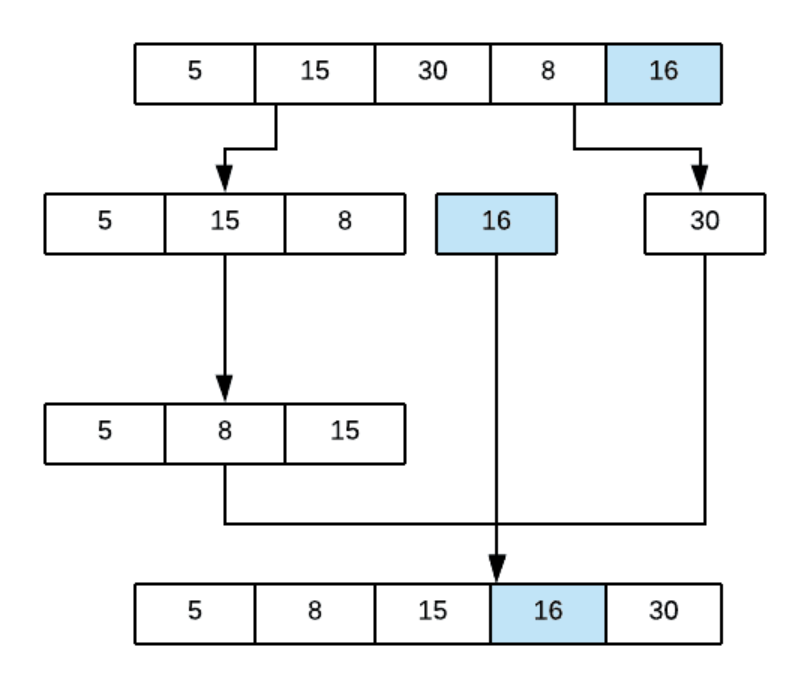
Select one:

A. Merge Sort

B. Selection sort

C. Quick sort

D. Bubble sort

A: Quick sort

What is the name of the algorithm for the following method ?

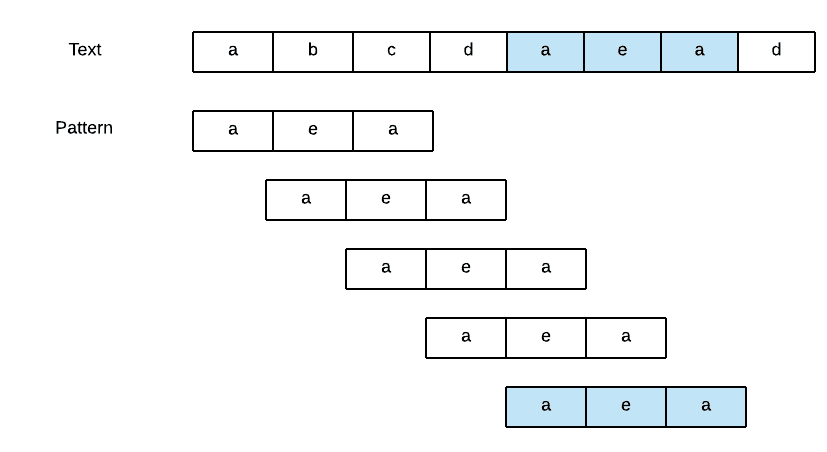
Select one:

A. Backtracking

B. Boyer - Moore

C. Greedy

D. Bruce Force

A: Bruce Force

Which of the problems or puzzles cannot be solved by backtracking method?

Select one or more:

A. travelling salesman problem

B. Knapsback

C. crossword

D. n-queen problem

A: A&B

只选了A，因为当时quiz时候找不到A。现在找发现好像C也找不到。

Crossword是通过边上给的提示来猜出一个N*N矩阵上的每个英文字母（含黑块，不用填）。因为和N-Queen一样只要得到一个解就能结束所以就能用backtrack。

Knapsback是背包问题，Greedy的案例。

travelling salesman problem根据Wikipedia解释就是解决*Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?*差不多就多点路线规划，个人理解应该需要Greedy

In Brute Force, the best-case running time is O ( nm )

A: F

The time complexity of brute force is O(mn), which is sometimes written as O(n*m) . So, if we were to search for a string of “n” characters in a string of “m” characters using brute force, it would take us n * m tries. 另外没有best-case的说法

Which of the following problems can be solved using a backtrack problem ?

Select one or more:

A. M colour map

B. N-Queen Problem

C. Knapsack

D. Tower of hanoi

A: A&B&D

相比上面的又多了俩游戏。

M colour map，没找到，但是个人理解应该指的是Four color theorem。用M种颜色不接触地涂满全部。

Tower of hanoi，汉诺塔。找出方法从左搬到右

Which of the following is true about Quick and Merge sort

Select one or more:

A. The quick sort is an internal sorting method where the data is sorted in main memory.

B. None of the above

C. Quick sort is more efficient and works faster than merge sort in case of smaller array size or datasets.

D. Merge sort is more efficient and works faster than quick sort in case of larger array size or datasets.

A: A&C&D

Quick Sort是一种内部排序方法（大概是说它不引入别的所以是内部？），其中数据在主内存中排序。√

在较小的数组或数据集的情况下，Quick Sort比Merge sort更有效且工作更快。√

在较大数组大小或数据集的情况下，Merge sort比Quick Sort更有效且工作更快。√

Which of the following is the most stable sort and has less time complexity ?

Select one:

A. Merge Sort

B. Quick Sort

C. None.

D. Bubble Sort

A: Merge Sort

Merge Sort的复杂度见下面

The average case and worst case complexities for Merge sort algorithm are

Select one:

A. O ( n^2 ), O ( n^2 )

B. O ( n^2 ), O ( nlog2(n) )

C. O ( nlog2(n) ), O ( nlog2(n) )

D. O ( nlog2(n) ), O ( n^2 )

A: C. O ( nlog2(n) ), O ( nlog2(n) )

Merge sort总是要迭代到

这样全部打散

For two objects x and y:

  • x is y is True
    if and only if
  • id(x) == id(y)

A: T

if and only if表示当且仅当所以正确

What things is an object associated with ?

Select one or more:

A. Value

B. Element

C. Object type

D. Data type

A: Data type , Object type

Val & Elem都与Obj无关

What are the main applications of tree data structure?

  1. Manipulate hierarchical data
  2. Make information easy to search (see tree traversal).
  3. Manipulate sorted lists of data
  4. Router algorithms
  5. Form of a multi-stage decision-making, like Chess Game.
  6. As a workflow for compositing digital images for visual effects

Select one:

A. 1, 2, 3, 4 and 6

B. 1, 3, 4, 5 and 6

C. 1, 2, 3, 4, 5 and 6

D. 1, 2, 3, 4 and 5

A: C. 1, 2, 3, 4, 5 and 6

答案是全对。当时没选6，没注意主语是workflow。用Tree来表示workflow是可以的

What does “+” mode mean, while working with files?

a. Append

b. Write

c. Read

d. Read and Write

A: d. Read and Write

选错选了a. Append。Append应该是"a" mode

Exam

总体简单，大量送分，全程基本都是写写写没选择

考了Depth First Inorder/Preorder/Postorder Tree 和Breadth First的List View（始料未及

还有手撸的selection sort

另外之前关注的valid/invalid/boundary test果然成考点

最后只有75，感觉考试扣分还是很严重